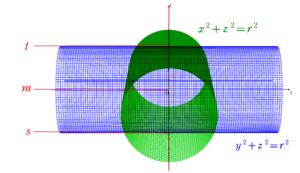
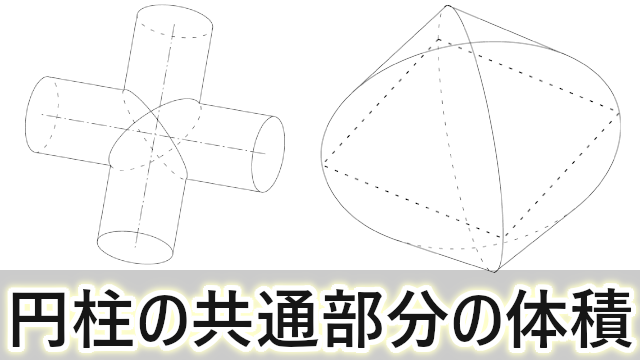
非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録 直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する いろいろな立体の問題 Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf 直交する3本の円柱の共通部分の 不等式で表された立体の体積、直交する円柱の共通部分の体積 スポンサーリンク 高校数学Ⅲ 積分法の応用(面積・体積・長さ) 検索用コード x0,x²y²1,0 z y²\ で表される立体の体積Vを求めよ$ 立体の形状をイメージしようとするのは無理があるた。視体積交差において、カメラの初期経度θを0~90度 の範囲で変化させ、シルエットを分割する提案手法と分割 しない場合について、視体積交差に要する計算時間を計測 した。その結果を図6に示す。また、カメラの初期経度θ =50度の場合の提案手法に
シンプソンの公式 応用編 Fukusukeの数学めも
円柱 交差 体積
円柱 交差 体積-視体積交差法と錯視立体 森口昌樹(明治大学先端数理科学インスティテュート) 視体積交差法とは,複数の2 次元図形( 3次元形状の輪郭を表している)から 次元形状を構築するため の基本的手法である.このとき,それぞれの2 次元図形に対応する視点情報も与えられているものとする.具体例で学ぶ数学 > 図形 > 円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 S は 2 ×円周率× 半径 × 半径 + 2 ×円周率× 半径 × 高さ このページでは、円柱の表面積について詳しく説明



シンプソンの公式 応用編 Fukusukeの数学めも
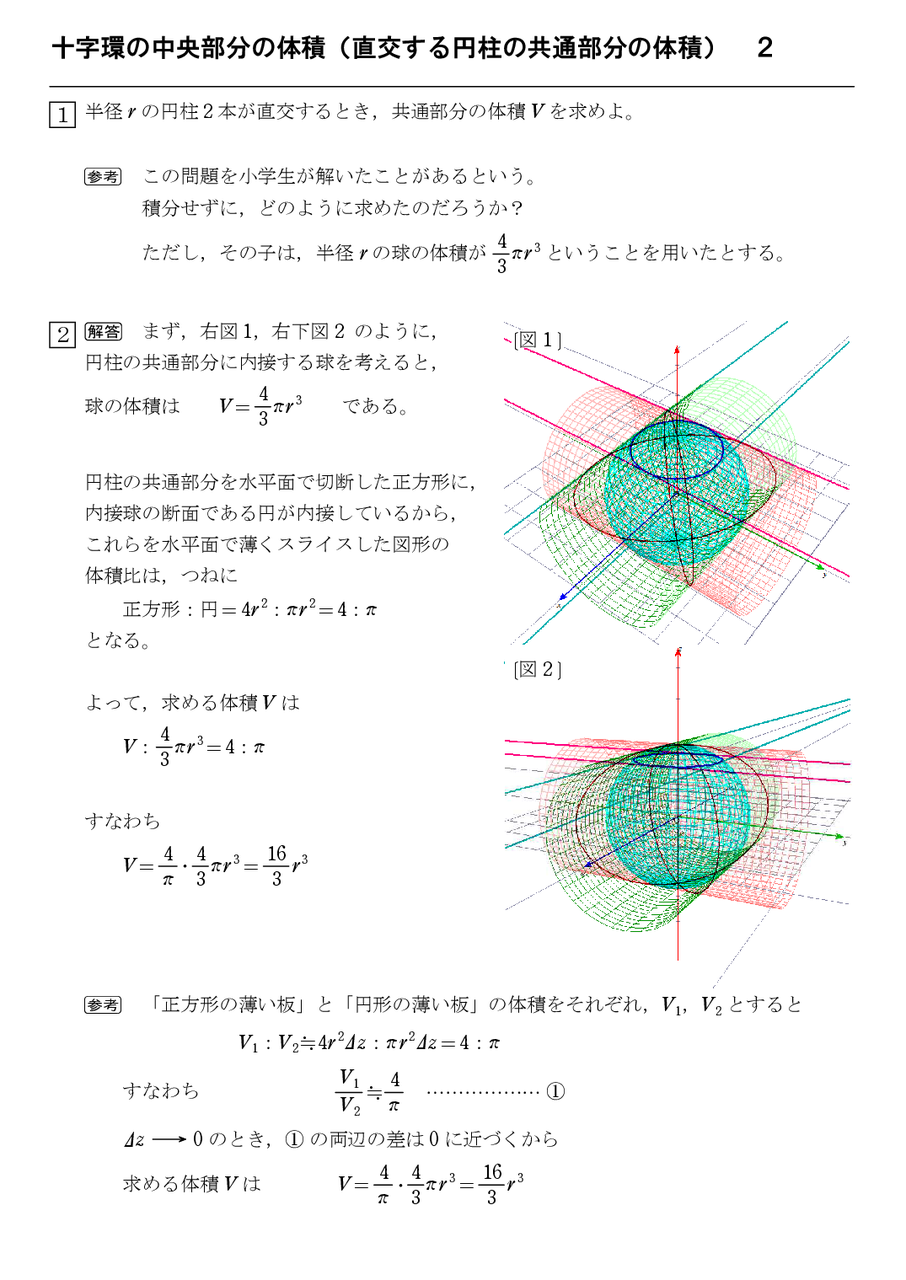
答え・解説 答え 3768cm 3 解説 展開図を組み立てると円柱になる。 側面の長方形の横の長さは,底面の円周の長さに等しい。 1256÷ 314 = 4 (cm) 4÷ 2 = 2(cm) より,底面の半径は2cm よって,元の立体の体積は,答533 円柱の交差部分の体積 底面の半径が 1 の直円柱2つが垂直に交差しているとき、その内部の共通部分の体積v は? 解答1 半径が 1 の球を内接させ、切り口が正方形になるように切断すれば、球の切り口である円が模型1(円柱から円錐へ・・・) 模型2(串刺し円柱) 模型3(BB弾で作る球) 模型4(角材で作る球)
問 3 70 (体積の計算) 2 つの円柱 の共通部分 の体積 を求めよ. 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換北海道大学 理系 a,bを正の実数とする。 xyz空間内の2点 A(a,0,0),B(0,b,1)を通る直線を lとし、直線lを z 軸のまわりに一回転して得られる曲面をMとする。 1P(x,y,z)を曲面M上の点とする。このとき x,y,zが満たす関係 式を求めよ。 2曲面Mと2つの平面 z = 0と z = 1で囲まれた立体の体積を求これを、 k=-1~1で積分して体積が得られる。 すなわち、 2 3つの円柱の場合 円柱の中心軸を x、y、z とし、原点で直交しているものとする。このときでき上がる物体
ここで、 直交する2円柱の共通部分を、 軸を含む平面で等分割して体積を求めます。 中心から距離がhとなる平面で切ったときに、 断面積が常に1となる立体は、 高さが1、底面積が1となる角柱が考えられます。 この立体の体積は1となります。 中心から距離がhとなる平面で切ったときに、 断面積がh^2となる立体は、 高さが1、底面積が1となる四角すいが考えられます。 この立体の体円柱2本・3本が交差している図形の観察 二円柱交差図形 三円柱交差図形 二円柱 三円柱 他の方法を含めて「パソコンで知る高校数学 ⅢC」にも収録しています。 Mahtematica トップページへ戻る非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録 Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf 直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する 円柱2本および3本の交差図形



直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法
(円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。上の基本問題をこの公式を使って求める (1) r=5、h=10 だから、V=π ×5 2 ×10=250π cm 3交差する2 円柱の共通部分の図示 「交差する2円柱の共通部分」と聞けば,半径の等しい2円柱が直交 していて,その共通部分の体積を積分で求めるという問題がすぐに思い浮 かぶであろう.この立体の図示は容易ではないが,ググればいくらでもそ球,表面積=1 円柱, 半径=3, 高さ=4 視覚表現のための色を指定する: ティファニーブルーの球 立体の特性を計算する: 体積v,高さ7の円錐の半径 底面積B,高さhの錐体の体積 もっと表示



いろいろな立体の問題




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ
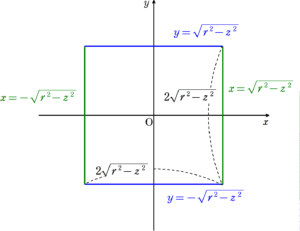
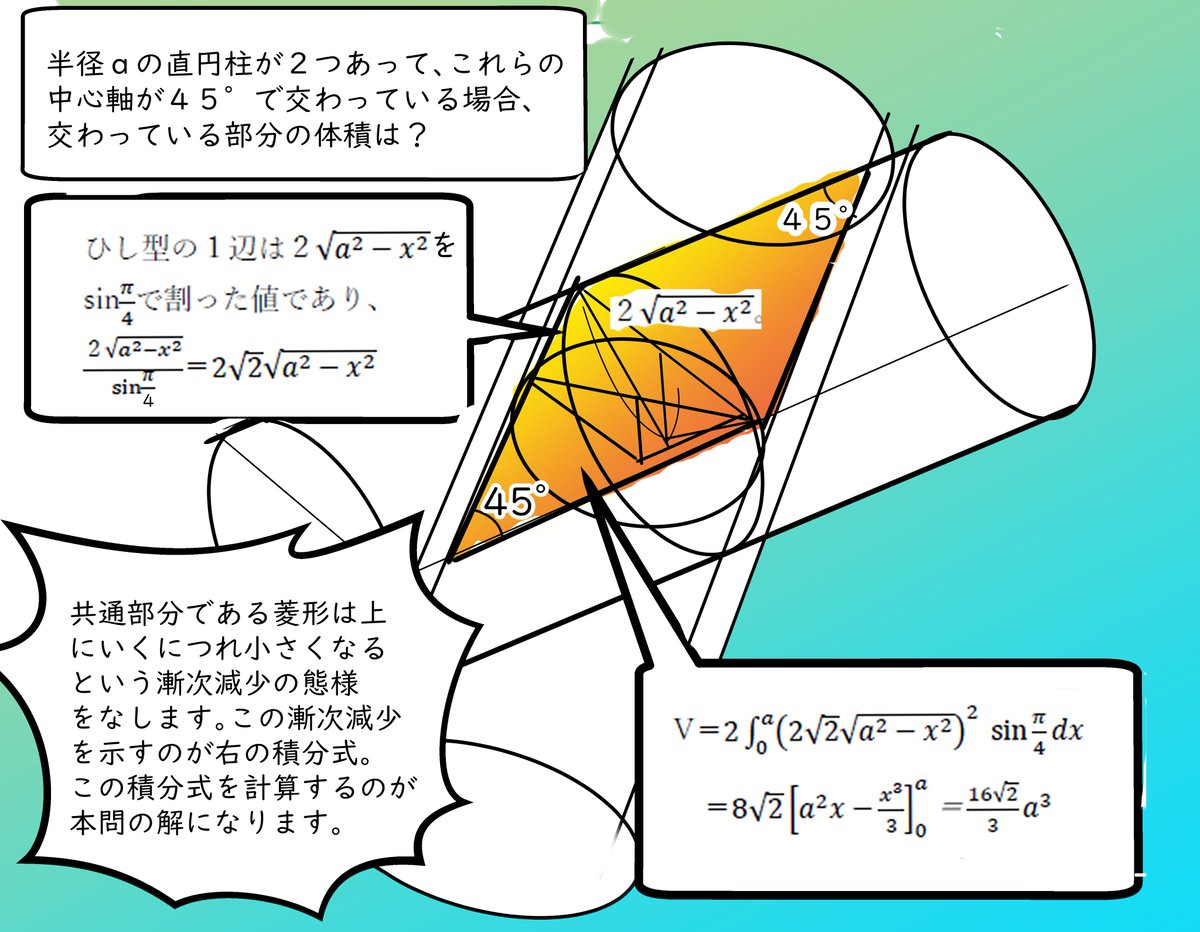
二円柱が交差する部分の体積 2つの直交している円柱 z2x2(a2 ① 2y2(a2 ② がある。 円柱①,②の共通部分の2円柱描画 xy 平面に平行な平面z=tによる切り口は共通部分描画 どのような図形か。また、切り口の面積を t の関数として表せ。両円の2交点を通過する直線の左側と右側に分けて体積を考えます。 左側の体積を ,右側の体積を とします。 を中心とする半径rの円: ・・・① を中心とする半径 の円: ・・・② ①の円から内側の部分、②の円から内側の部分、両者の共通部分をx軸のまわりに回転させた立体の体積が です。正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱




重積分5 三つの交差する円柱の領域の体積 数学 微分積分学 Mathematics Youtube



1
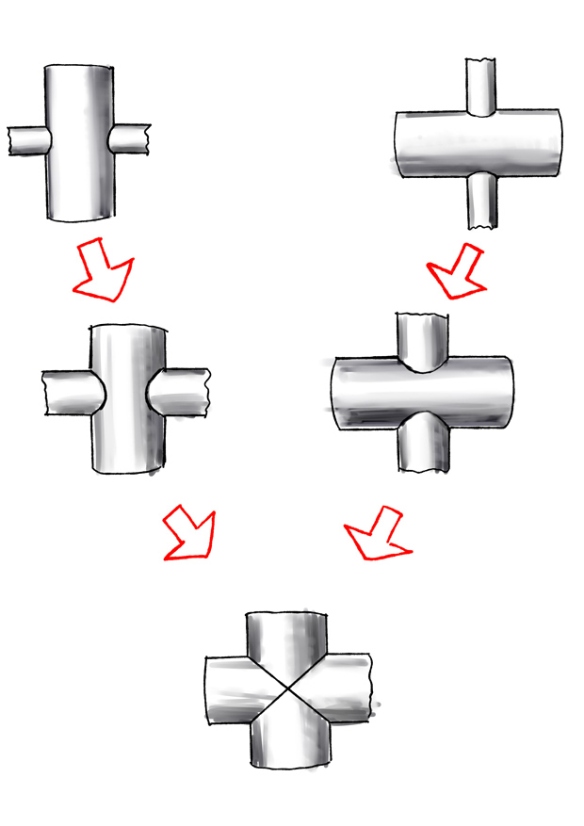
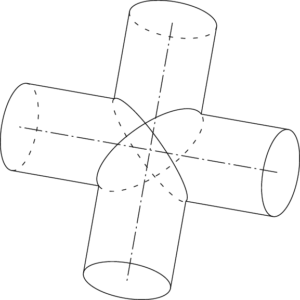
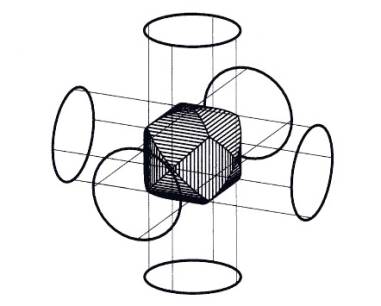
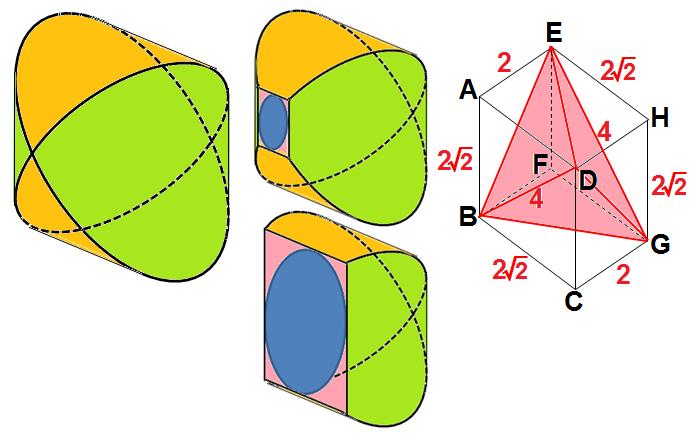
体積における置換積分を理解していれば次の問題は難しくありません. 例題3 立体A,B,Cをそれぞれ半径の1の直円柱とする.A,B,Cのどの2つの中心軸も直交するとき, 3つの円柱の共通部分の体積 第9章 交差円柱とアルキメデスの意図 第10章 交差円柱:失われた証明 第11章 補章 球だけでなく回転放物体、回転双曲体、爪型(斜切円柱)、交差円柱などさまざまな立体の体積を求めていることがおわかりだろう。 3つの直交する円柱の共通部分の体積 更新日: 年12月6日 公開日: 19年8月6日 2次試験対策 上野竜生です。 今回は3つの直交する円柱の共通部分の体積を紹介します。 2つのときとほぼ同様ですが 計算が大変になることと,それをうまく回避する技も



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu3ko Pdf



円柱とは コトバンク
533 円柱の交差部分の体積 底面の半径が 1 の直円柱2つが垂直に交差しているとき、その内部の共通部分の体積V は? ★ コメントをお待ちしています(解答だけでも構いませんが、解き方も示されている 3円柱が直交する交差部分の体積 『rを正の実数とする。 xyz空間において を満たす点全体からなる立体の体積を求めよ。 』 05年の東大の入試問題です。 3円柱が交差している状況です。 x = t の断面を考えて解くのです。 そのイメージを生徒に伝える次に,3本の直円柱の共通部分の体積を求めます。 問題2 直交する半径1の3本の円柱の共通部分の体積を求めよ。 〔解答〕座標を導入する。つまり,題意の図形は 22 22 22 1 1 1 xy yz zx ≦ ≦ ≦ を満たす点(, ,)x yzの存在領域である。



Deadliner デッドライナー 創作同盟 受験勉強 Illustrations イラスト王国 勉強垢 Digitalart Artistontwitte 理系 大学受験 体積 Volume 断面形状 冬の創作クラスタフォロー祭り 数3 積分 Integral 絵描きの輪 Artwork Art 日本女子大




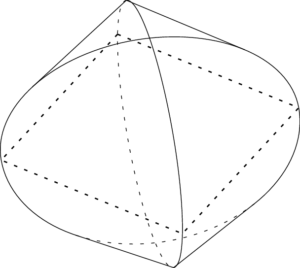
非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
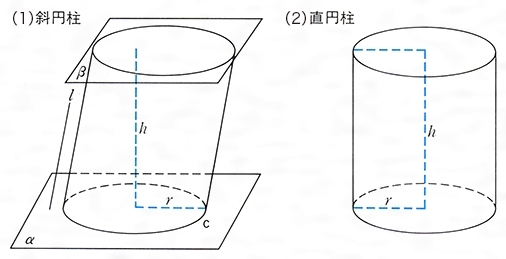
底面の半径a,高さがhの2つの斜円柱が下底を共通し,上底が外接している.この2つの斜円柱の共通部分の体積を求めよ. 解答 斜円柱の底面の半径を1,高さを1として求めればよい(これは,出た結果をa 2 h倍すればよいからです). 2つの斜円柱の共通の円柱 座標系(えん これは上記の基準平面と基準軸の交点になる。 円筒極座標系を含む多くの問題において線素および体積要素がこの座標系でどのように表されるかを知っていることは有意である(それにより曲線経路や体積を含む問題を積分によっ 交差する円柱の共通部分の体積を求めさせる問題は手ごろな積分の問題として時々出題されます。今回はこの "Steinmetz solid" をテーマに体積や表面積について詳しく解説します。非回転体の求積の代表例なのでしっかり押さえておきましょう!



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu3ko Pdf



円柱の斜め切断
東大理系数学'05年前期 6 東大理系数学 '05 年前期 6 r を正の実数とする。 xyz 空間において をみたす点全体からなる立体の体積を求めよ。 解答 この問題は過去にも類題があります。 問題文の書き方はかなり違いますが、実質的に、 '94 前期 3 , '98東京都 eikiさんからの解答。 確報です。 微小高さの円柱(正4角柱)を中心角の関数と見て3角関数で積分しようと苦労していたのですが、 より底面積を計算すれば簡単に積分できました。 したがって、球の体積:この立体の体積 =π:4 だから体積が 1 つ与えられたとき、表面積が最小となる円柱(または、表面積が 1 つ与えられたとき、体積が最大となる円柱)では h = 2r という関係が成り立つ。これは半径 r の球に外接する円柱であり、球と円柱の体積の比と表面積の比がどちらも 23 となる。



半径1で等しい三円柱が交差してできる共通部分の体積を求める問 Yahoo 知恵袋




4 三本円柱交差 05理 Matemata Note
立体の体積&容積および諸数値 V=容積、S=表面積、As=側面積、Ab=底面積、x=底面より重心までの距離 寸 法 容積および諸数値 寸 法 容積および諸数値 V=a 2 S=6a 2 As=4d 2 正多角形 a=辺長 三角形の面積の積分で求める x^2y^2\text≦1,0\text≦ z\text≦ 3 x2 y2≦1,0≦z≦3 を同時に満たす円柱を考える。 H H とする。 円柱 (0,1,0) (0,1,0) を含む方の体積を求めよ。 こういう問題は実際に図を描いてみることが大事。 この立体の体積は、三角形の面積を<円柱貫通体について> 積分を応用して円柱貫通体の体積Vを求める。 2本の円柱が交わった部分の立体の体積を求める有名な問題でが、高校生3年生時に説明を聞くまでは、立体 の形がイメージできなかったのではないでしょうか?



Http My Reset Jp Gok Math Pdf Analysis 16awan15 Pdf



体積積分 交差立体 京極一樹の数学塾
底面の半径が r の円柱を直角に交差させたときの共通部分の体積を求めよ。 高校数学の積分でおなじみの問題ですね。 解けるかどうかはともかく、この図形がどんな形をしているのかなかなかイメージができず苦労した記憶があります。 (「球体になるんじゃないの?



不可思議な立体



1



いろいろな立体の問題




共通部分の体積 数 積分法 現大手予備校講師の5分でわかる 高校数学 Youtube




直交2円柱 3円柱の表面積を簡単に求める方法 Den Of Hardworking



17 図形の諸量 17 2 単純要素への分割と合成 17 2 3 単純な形状のマスプロパティの計算 図17 2 相貫円柱 宮崎 単純な立体図形の造形で最も基本的な形状単位は 任意の平面図形を底とした柱です 側面から見る図形は矩形です どの側面から見ても




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



西三数学サークル通信30号



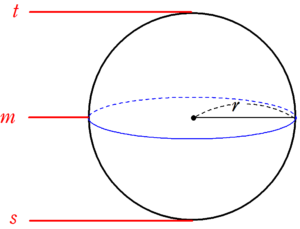
十字環の中央部分の体積 直交する円柱の共通部分の体積 2 怜悧玲瓏 高校数学を天空から俯瞰する



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法



3円柱が直交する交差部分の体積 数学キノシタの家庭教師な日々




5 2つの円柱が交差した部分の体積




シンプソンの公式 応用編 Fukusukeの数学めも




書記が数学やるだけ 29 体積をいろんな積分で解く 鈴華書記 Note



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf



Nekodamashi Math Blog Ss Blog Jp 17 11 03



シンプソンの公式 応用編 Fukusukeの数学めも



Http Www10 Plala Or Jp Mondai Columun Kousa Pdf




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



直交する円柱



円柱2本および3本の交差図形



いろいろな立体の問題



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する



交差する円柱の共通部分 前川淳 折り紙 かたち散歩




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録




高校積分で 三つの交差する円柱の領域の体積を求めます 数学 微分積分 Youtube



Http My Reset Jp Gok Math Pdf Analysis 16awan15 Pdf



3円柱が直交する交差部分の体積 数学キノシタの家庭教師な日々
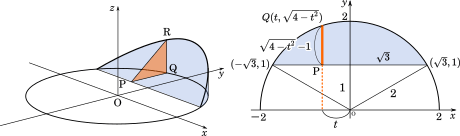



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



交差する円柱の共通部分 前川淳 折り紙 かたち散歩



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



天秤の魔術師 アルキメデスの数学 林栄治 斎藤憲 とね日記



直交する円柱



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf



いろいろな立体の問題




直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか



図のように 底面の直径が2で長さが充分に長い2つの円柱を中心軸が直交するよう Yahoo 知恵袋




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



直交する円柱




シンプソンの公式 応用編 Fukusukeの数学めも



いろいろな立体の問題
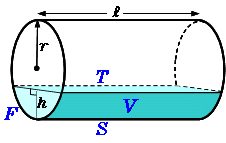



一部が欠けた直円柱の体積 高精度計算サイト




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



答533 円柱の交差部分の体積 解答集



東大理系数学 05年前期 6



体積積分 Of 京極一樹の数学塾会員頁



体積積分 交差立体 京極一樹の数学塾
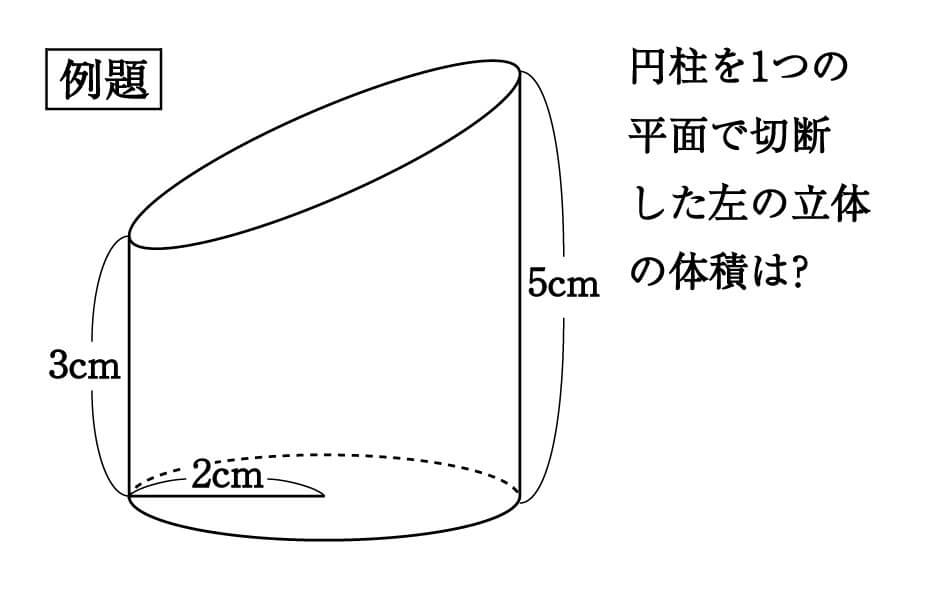



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



体積積分 交差立体 京極一樹の数学塾



半径1で等しい三円柱が交差してできる共通部分の体積を求める問 Yahoo 知恵袋




4 三本円柱交差 05理 Matemata Note



ヘルプ 概要 プリミティブ 3d ソリッドを作成する




55 体積 直交する円柱 アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




体積の求め方 回転体ではない立体を積分で 数学の偏差値を上げて合格を目指す




4 三本円柱交差 05理 Matemata Note




ねこ騙し数学




3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す



直交する3円柱を作ってみましょう オモシロ算数



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu3ko Pdf



3 13 体積の計算



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書



1




3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す




直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか




共通部分の体積 数 積分法 現大手予備校講師の5分でわかる 高校数学 Youtube



いろいろな立体の問題



直交した2つの円柱の共通部分の体積を計算したいのですが 添付図 Yahoo 知恵袋




高校数学 不等式で表された立体の体積 直交する円柱の共通部分の体積 受験の月




直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する
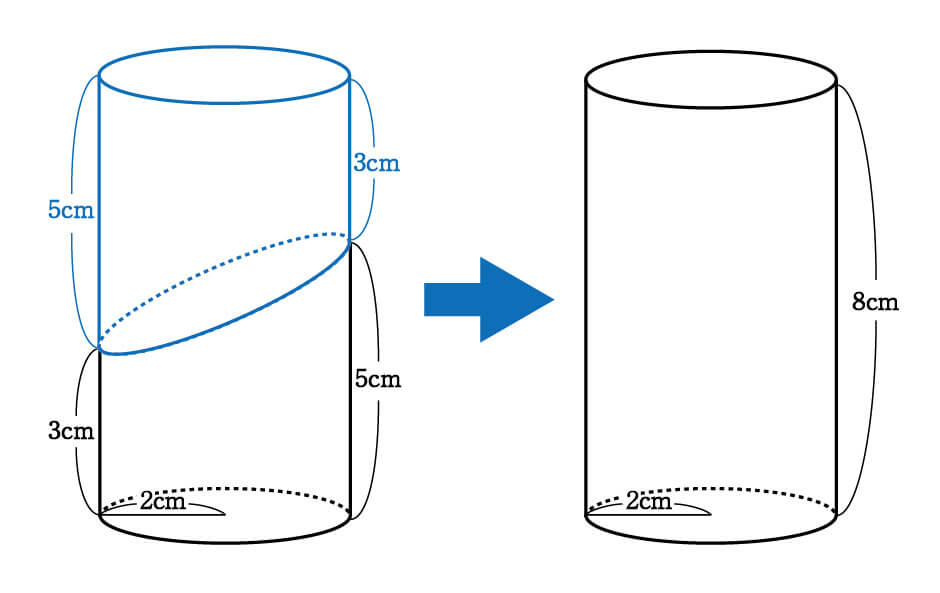



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




答533 円柱の交差部分の体積 解答集




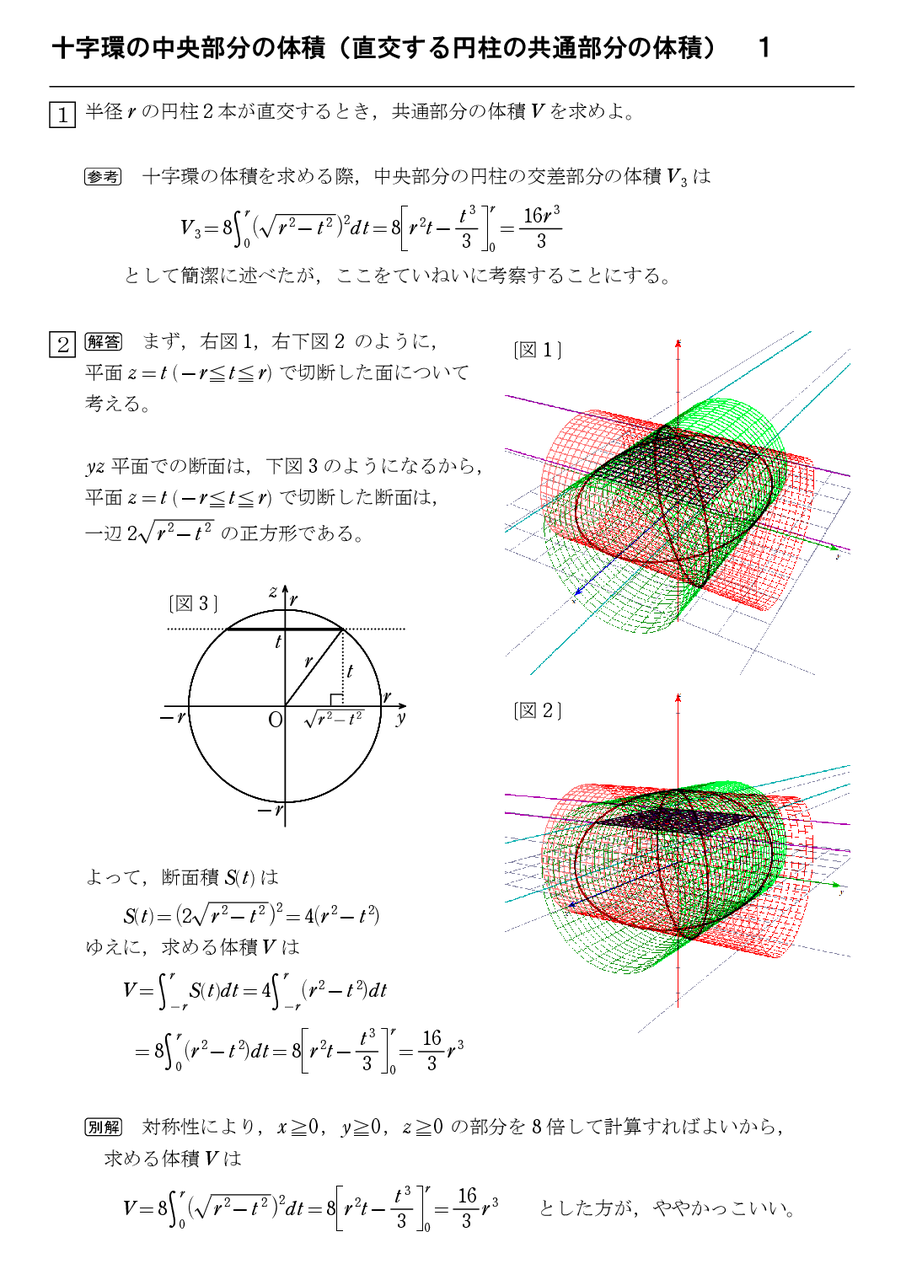
十字環の中央部分の体積 直交する円柱の共通部分の体積 1 怜悧玲瓏 高校数学を天空から俯瞰する



円柱の斜め切断




直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか
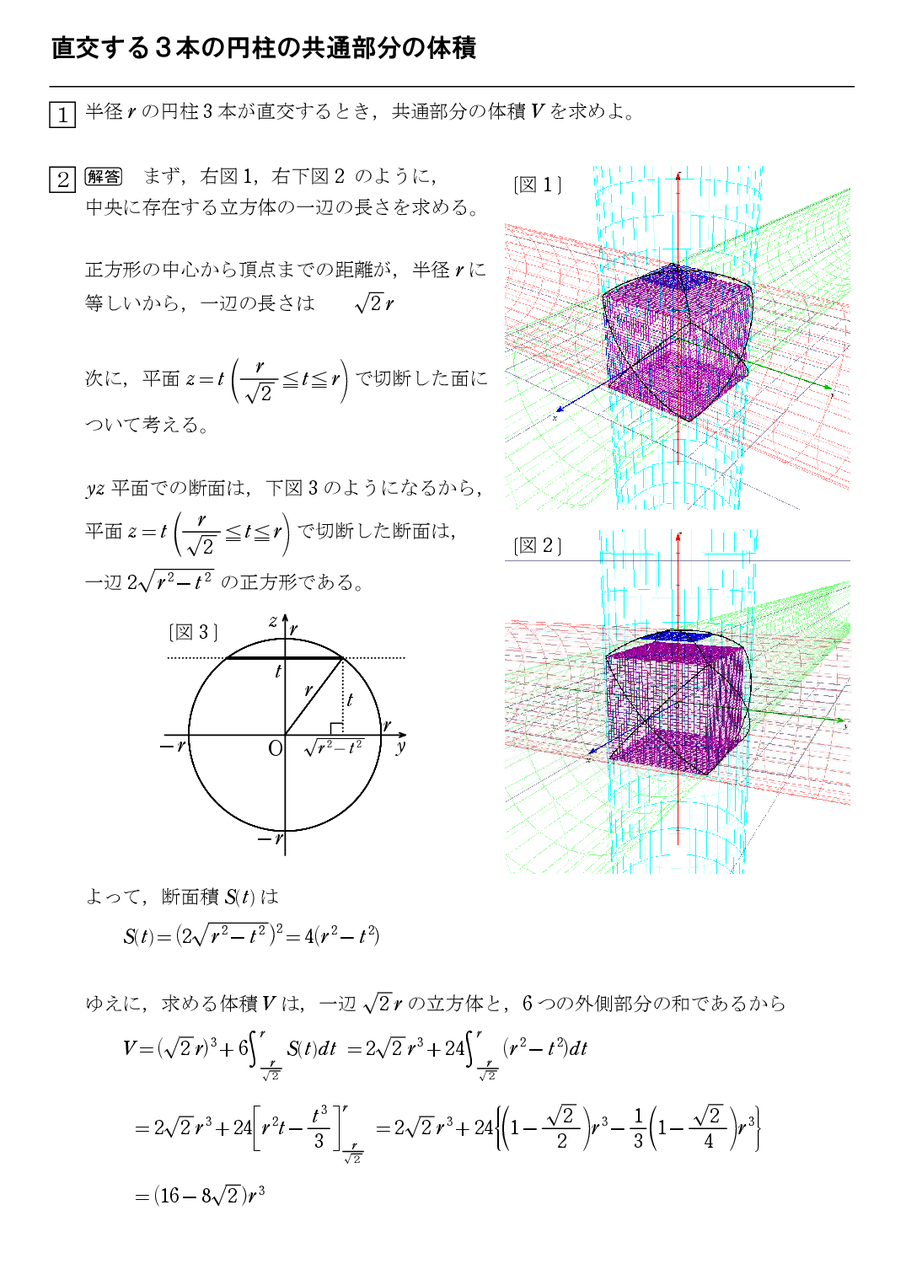



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する




ねこ騙し数学



不可思議な立体
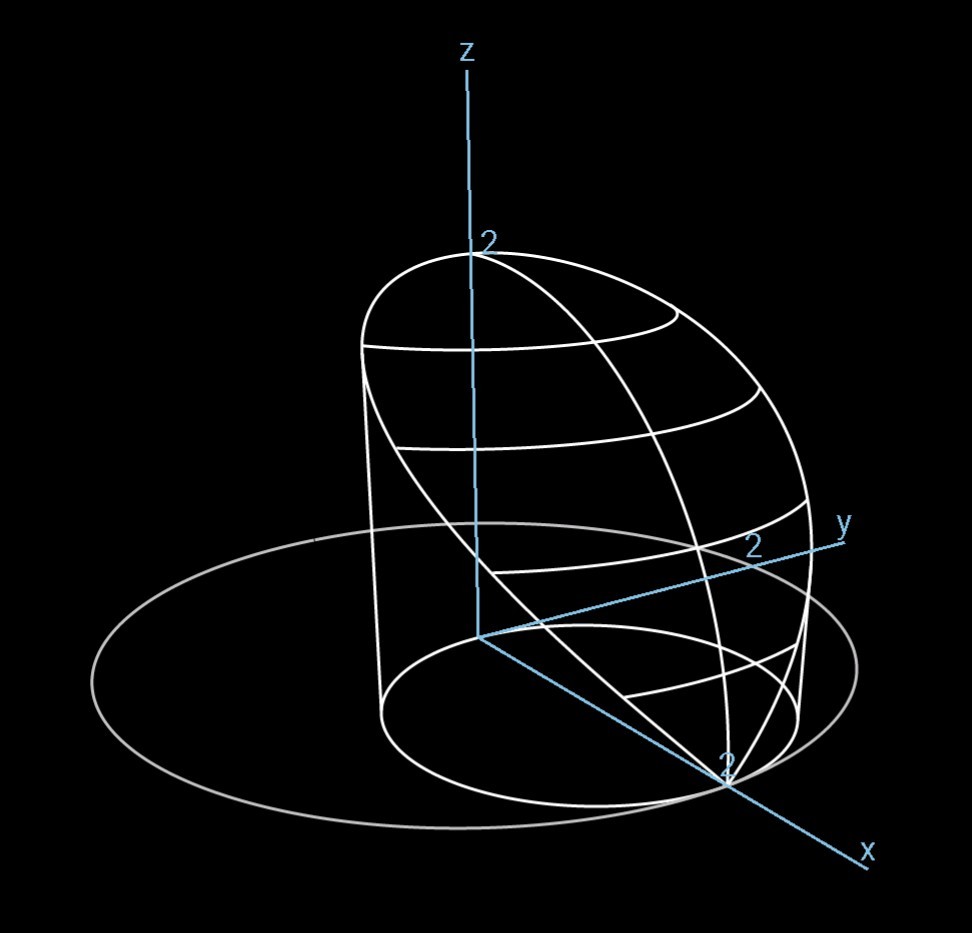



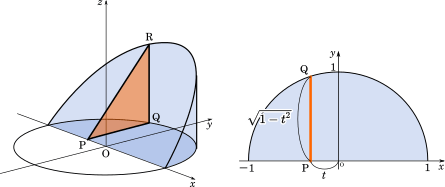
2 半球と円柱の交わりの体積を で求める 齊藤数学教室 算数オリンピックから大学数学入門
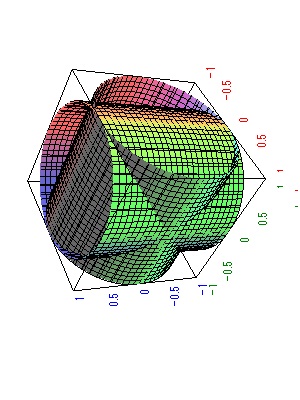



直交する2円柱を作る コ コ ロで遊ぶ算数教室



1



Http My Reset Jp Gok Math Pdf Analysis 16awan15 Pdf




直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する
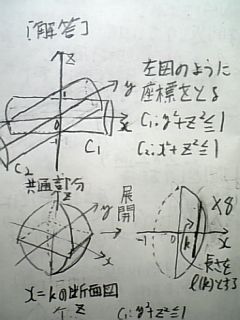



直交する円柱の共通部分の体積と表面積 わんこら日記



体積積分 交差立体 京極一樹の数学塾




重積分4 二つの交差する円柱の領域の体積 数学 微分積分学 Youtube



0 件のコメント:
コメントを投稿