200以上 y=ax^2 parabola 784633-Y ax 2 parabola open

A normal is drawn to a parabola y 2 = 4 a x at any point other than the vertex and it cuts the parabola again at a point whose distance from the vertex isFind vertex, axis ,focus , directrix, latusretum of parabola 4 y 2 1 2 8 − 2 a y 6 5 = 0 View solution Find the focus and the equation of the directrix of the parabola 2 x 2 3 x − 2 y − 1 = 0 If y = ax^2 bx c represents a parabola with vertex A as shown in the figure and b^2 = 2(b 2ac), asked in Mathematics by Mousam (528k points) jee;

Graphing Parabolas

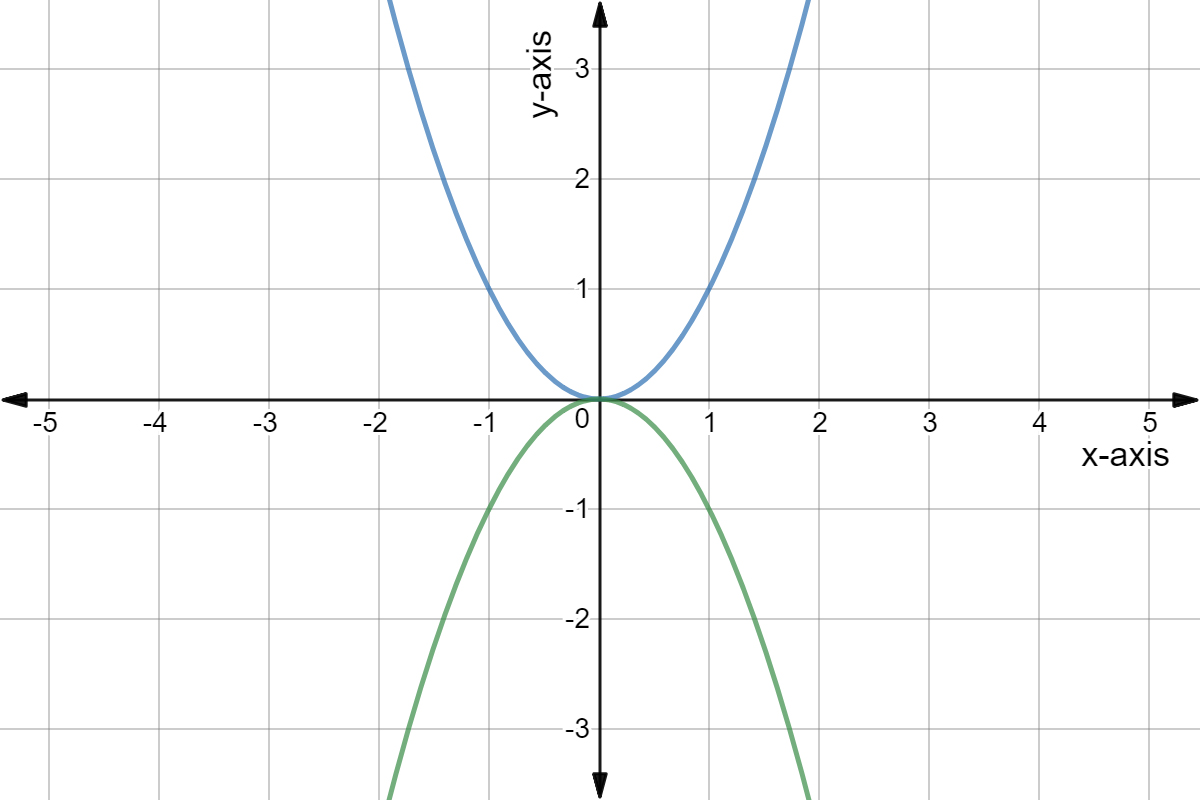
Y ax 2 parabola open

Y ax 2 parabola open-0 votes 1 answer Show that y = ax^2 bx c, a ≠ 0 represents a parabola and find its vertex, focus, directrix and latus rectum The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bx c Our job is to find the values of a, b and c after first observing the graph

Question 1 The Parabola Is Described By The Quadra Gauthmath

Given equation of parabola is y = a x 2 − 6 x b Since it passes through (0, 2) 2 = 0 b ⇒ b = 2 Also, d x d y = 2 a x − 6 So, slope of tangent at (x = 2 3 ) = 2 a (2 3 ) − 6 = 3 a − 6 Since the tangent at x = 2 3 is parallel to x − axis ⇒ 3 a − 6 = 0 ⇒ a = 2 Hence, a = 2, b = 2The graph of mathy^2=ax/math will be parabola Two graphs are shown below for positive and negative values of matha=1/math matha=1/math matha=1/mathOne formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form Standard Form If your equation is in the standard form $$ y = ax^2 bx c $$ , then the formula for the axis of

Exploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdThe best known parabolas, are those whose vertex is at the origin of coordinates, this parabola has the general equation given by the expression {eq}y = ax^2 {/eq} Answer and Explanation 1 y = ax 2 c, where a≠ 0 In the parent function, y = x2, a = 1 (because the coefficient of x is 1) When the a is no longer 1, the parabola will open wider, open more narrow, or flip 180 degrees Examples of Quadratic Functions where a ≠ 1

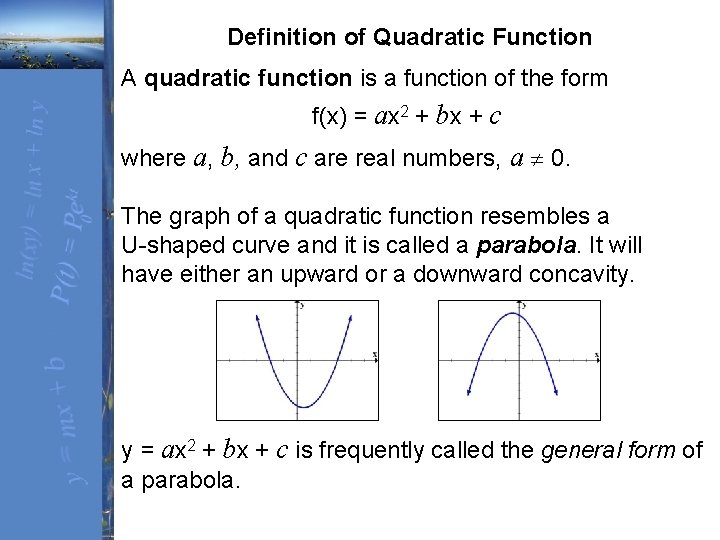
For example, a univariate quadratic function has the form f = a x 2 b x c, a ≠ 0 {\displaystyle f=ax^{2}bxc,\quad a\neq 0} in the single variable x The graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the yaxis, as shown at right If the quadratic function is set equal to zero, then the result is a quadratic equation The solutions to the A parabola y = ax 2 bx c crosses the x axis at (α, 0) (β, 0) both to the right of the originA circle also passes through these two pointsA quadratic function in the form f (x) = ax2 bxx f ( x) = a x 2 b x x is in standard form Regardless of the format, the graph of a quadratic function is a parabola The graph of y=x2−4x3 y = x 2 − 4 x 3 The graph of any quadratic equation is always a parabola

Graphing Parabolas My Ccsd

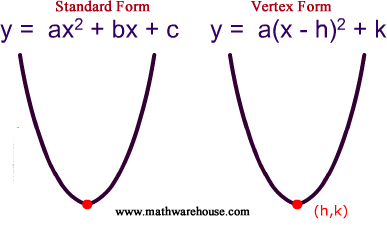
Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph

 So, the coordinates of the vertex are V = (x v , y v) = (5/2 , – 1/4) or (2,5 , 0,25) yaxis interception point The parabola intercepts the yaxis at the value of the c coefficient In the function above, the value of c = 6, therefore, the parabola intercepts the yaxis at the point (0, 6) Graph of a quadratic function As said before, the graph of a quadratic function is known as aA wire bent as a parabola y = ax 2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane x, y At the moment t = 0 a connector starts sliding translationwise from the parabola apex with a constant acceleration w (Fig 378) Find the emf of electromagnetic induction in the loop thus formed as a function of ySal rewrites the equation y=5x^2x15 in vertex form (by completing the square) in order to identify the vertex of the corresponding parabola Sal rewrites the equation y=5x^2x15 in vertex form (by completing the square) in order to identify the vertex of the corresponding parabola

Graphing Parabolas

Graphing Parabolas

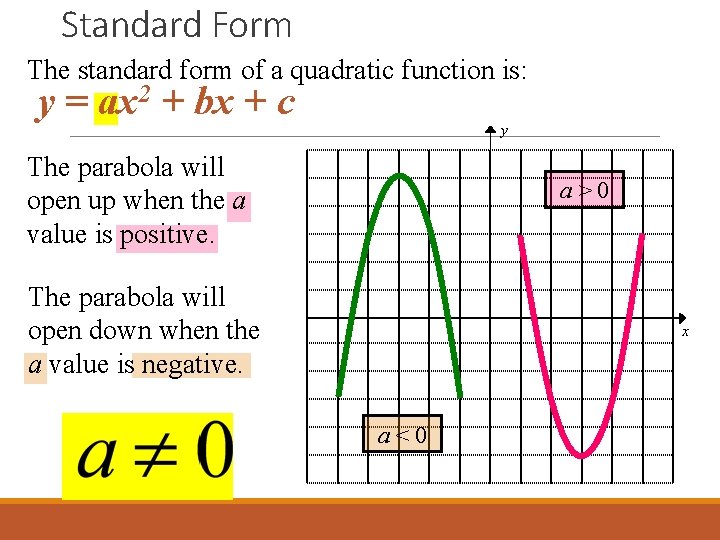
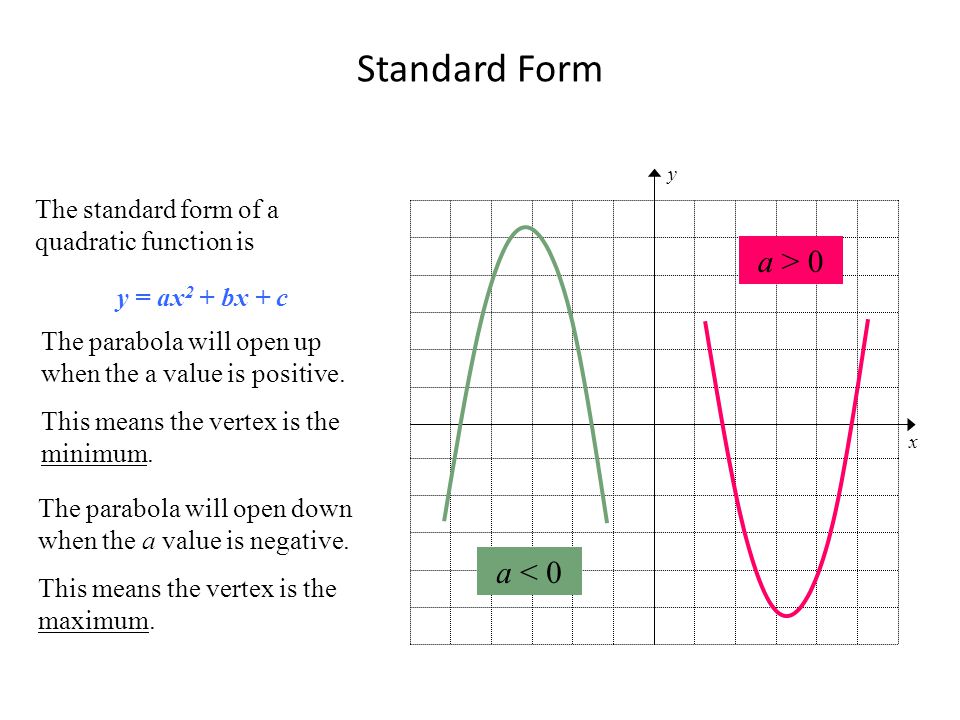
In this video we're going to talk about one of the most common types of curves you will see in mathematics and that is the parabola and the word parabola sounds quite fancy but we'll see it's describing something that is fairly straightforward now in terms of why it is called the parabola I've seen multiple explanations for it it comes from Greek para that root word similar to parable youThe general form of a quadratic is "y = ax 2 bx c" For graphing, the leading coefficient " a " indicates how "fat" or how "skinny" the parabola will be For a > 1 (such as a = 3 or a = –4 ), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values 5 How to Find the the Directionthe Graph Opens Towards y = ax2 bx c Our graph is a parabola so it will look like or In our formula y = ax2 bx c, if the a stands for a number over 0 (positive number) then the parabola opens upward, if it stands for a number under 0 (negative number) then it opens downward 6

Quadratic Systems A Line And A Parabola Video Khan Academy

Graphing Quadratic Functions Ma 912 A 7 1

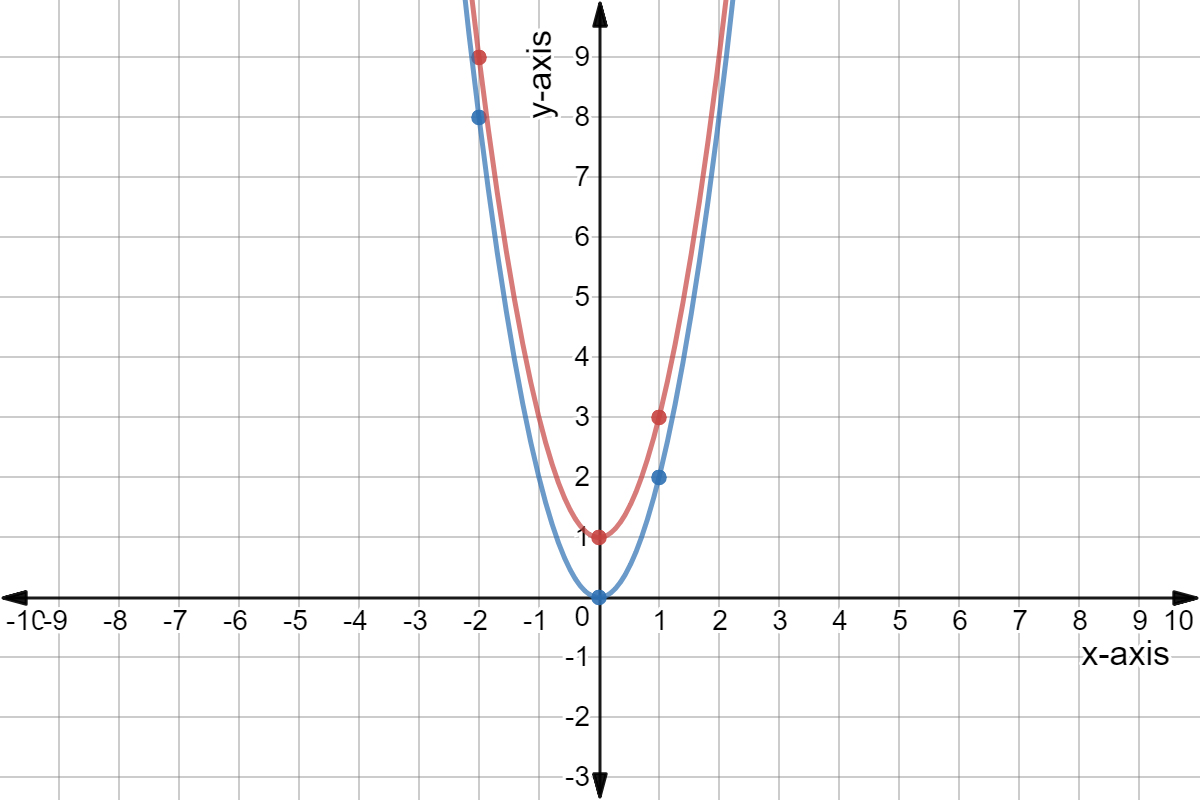
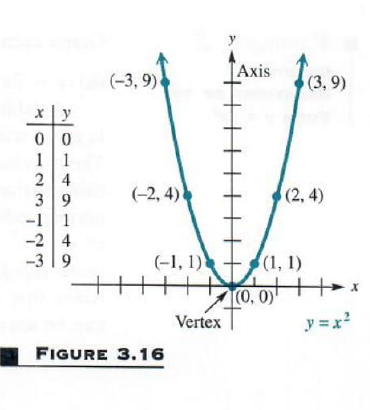
The value of a controls how fast the parabola rises The sign of a controls its direction, opening upward or downwardWhen first looking at the equation y = ax^2 we know that we will be graphing a parabola A parabola is the set of all points that are the same distance from a fixed line called the directrix and a fixed point called the focus, that is not located on the directrixThe graph of a quadratic equation in two variables (y = ax 2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot

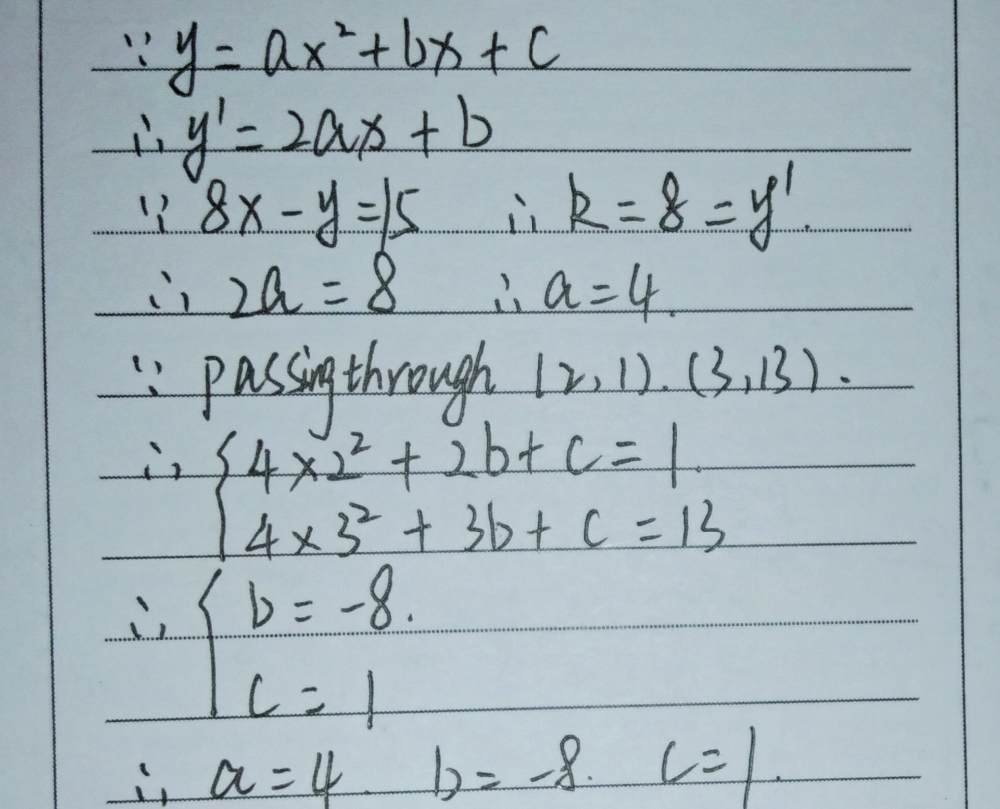
Determine The Coefficients A B And C Of The Para Gauthmath

Parabola Y Ax 2 Worksheet With Solutions Teaching Resources

A parabola y = ax^2 bx c crosses the x axis at (alpha, 0) (beta, 0) both to the right of the origin A circle also passes through these two points The length ofFor y = 2x^2, let us pick (2, 18) and (5, 50) Then for y = 10x^2, we will pick (2, 40) and (5, 250) y = 2x^2 Rate of decrease = (50 18)/(5 2) = 32/ 3 = y = 10x^2 Rate of decrease = (250 40)/ (5 2) = 210/3 = 70Caso particolare di una parabola con delta positivo, in cui il termine noto c è nullo📱FACEBOOK https//wwwfacebookcom/matematicale📱INSTAGRAM https//ww

Find The Parabola Of The Form Y Ax 2 B Which Best Fits The Points 1 0 4 4 5 8 Mathematics Stack Exchange

Quadratic Function

Caso particolare di parabola con coefficiente di primo grado b nullo, in cui il vertice è sull'asse delle y📱FACEBOOK https//wwwfacebookcom/matematicale?Alternative form for quadratic equations We can also write the quadratic equation in the form y = a(x– p) 2 q The effect of p is still a horizontal shift, however notice that For p > 0, the graph is shifted to the right by p units For p < 0, the graph is shifted to the left by p units The equation of parabola can be expressed in two different ways, such as the standard form and the vertex form The standard form of parabola equation is expressed as follows f (x) = y= ax2 bx c The orientation of the parabola graph is determined using the "a" value If the value of a is greater than 0 (a>0), then the parabola graph

1

Quadratic Graph Example Y Ax C Expii

The form y = ax 2 bx c provides the yintercept of the graph, the point (0, c), and the quadratic formula is based in the values of a, b, and c to find the zeros of the graph Example The graph of y = 2x 2 4x 6 has yintercept (0, 6) and using the quadratic formula its zeros areA 2 B 1 C 1/2 1 See answer yamadoo74 is waiting for your help Add your answer and earn points mariacsinning mariacsinning Answer B 1 Stepbystep explanationFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience

Parabola Wikipedia

View Question The Parabola With Equation Y Ax 2 Bx C Is Graphed Below

The Parabola Algebraic Definition of The Parabola Recall that the standard equation of the parabola is given by y = a (x h) 2 k If we are given the equation of a parabola y = ax 2 bx c we can complete the square to get the parabola in standard form Geometry of the Parabola We can define a parabola as followsAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Quadratics

This Is What The Problem Says Assuming All Parabolas Are Of The Form Y Ax 2 Bx C Drag And Drop The Brainly Com

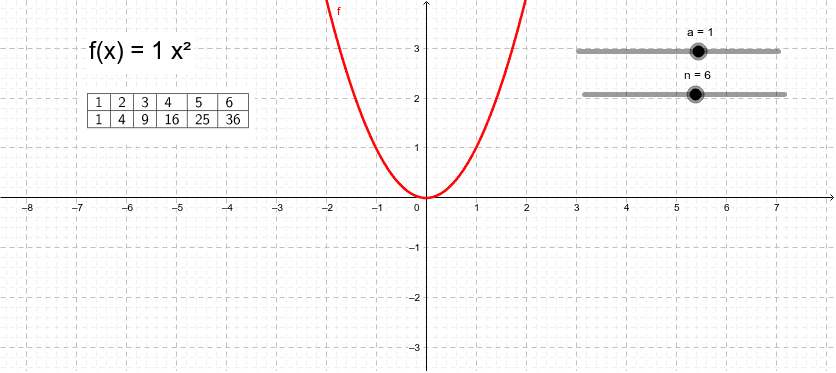
Interactive lesson on the graph of y = ax² bx, including its roots, axis of symmetry, and vertex, using sliders Show that y = ax^2 bx c, a ≠ 0 represents a parabola and find its vertex, focus, directrix and latus rectum Sarthaks eConnect Largest Online Education Community The line of symmetry of the parabola whose equation is y = ax^2 4x 3 is x = 2 What is the value of "a"?

What Is The Equation Y Ax 2 X Of The Parabola That Is Tangent To The Line With Equation Y 3x 1 Show Your Work Quora

How To Analyze A Parabola 6 Steps With Pictures Wikihow

Tha answer is 3) if a is positive, the parabola opens upward You can see that when you imagine what happens when x is large In that case bx c is small compared to ax^2, and the value of the function is dominated by the terms ax^2 x^2 is positive always, so the sign of ax^2 is given by a Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeGiven a quadratic function \(f(x) = ax^2bxc\), it is described by its curve \y = ax^2bxc\ This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation \(y=x^2

Question 1 The Parabola Is Described By The Quadra Gauthmath

Quadratic Function Wikiwand

 Given the Equation #color(red)(y=f(x)=4x^2# A Quadratic Equation takes the form #color(blue)(y=ax^2bxc# Graph of a quadratic function forms a Parabola The coefficient of the #color(red)(x^2# term (a) makes the parabola wider or narrow If the coefficient of the #color(red)(x^2,# term (a) is negative then the parabola opens down The term Vertex is used Best Answer Suppose that we have an equation y=ax^2bxc whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0)This set of parabolas introduces many interesting effects Firstly, one can see that the y = ax 2 bx c where a, b, and c are all positive and the similar parabola where 'a' is the additive inverse, one observes that these two parabolas are inverses and both shifted to opposite quadrants around the line of symmetry y=2x2

Exploring Parabolas Y Ax 2 Bx C

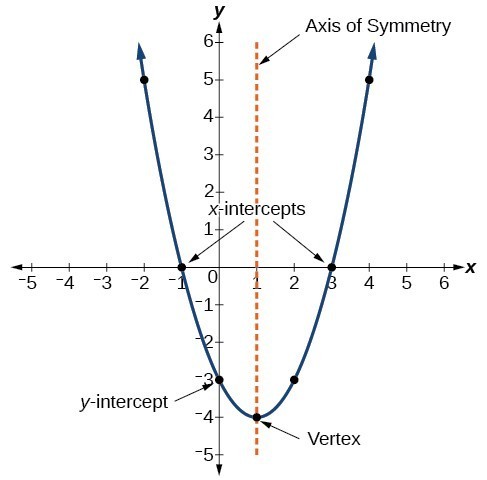
Characteristics Of Parabolas College Algebra

The Graph of y = ax2 bx c 393 Lesson 64 The Graph of y = ax2 bx c Lesson 6–4 2 BIG IDEA The graph of y = ax bx c, a ≠ 0, is a parabola that opens upward if a > 0 and downward if a < 0 Standard Form for the Equation of a Parabola Homer King hits a high–fl yWhy the focus of the parabola y=ax^2 is the point (0,1/(4a)), a presentation by Sunil Koswatta, Professor of Mathematics at Harper College, Palatine, IllinoisHttp//wwwlezionidimateit http//wwwwikimateit In questa lezione cominciamo a definire la parabola e successivamente trattiamo il caso specifico di una p

To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com

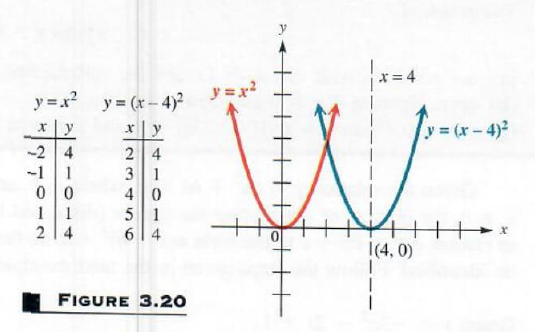
Solve Quadratic Relation Parabolas Step By Step Math Problem Solver

 I have trouble grasping some basic things about parabolas (This should be easily found on Google, but for some reason I couldn't find an answer that helped me) I know one simple standard equation

Vertex And Intercepts

1

Quadratic Function Wikipedia

What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora

Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download

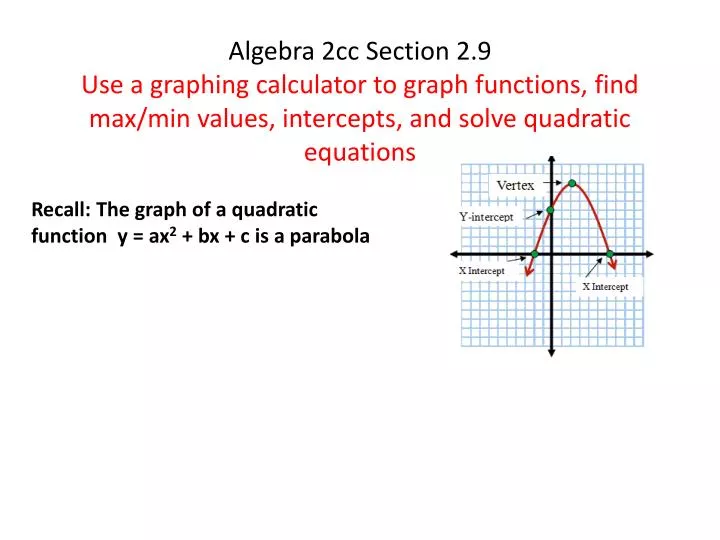
Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id

Graphing Parabolas

Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com

Parabola Y Ax 2 Geogebra

The Department Of Mathematics Education J Wilson Emat 6680 Assignment 2 Quadratics By Hulya Kilic In This Assignment I First Constructed The Graphs Of Parabolas Having Standard Form Y Ax2 Bx C Here The Graphs Of The Parabolas That I Chose Then

Quadratic Function Y Ax2 Bx C When A Is Sutori

5 1 Quadratic Functions Functions Siyavula

Quadratic Graph Example Y Ax Expii

Maths First Institute Of Fundamental Sciences Massey University

Solve Quadratic Relation Parabolas Step By Step Math Problem Solver

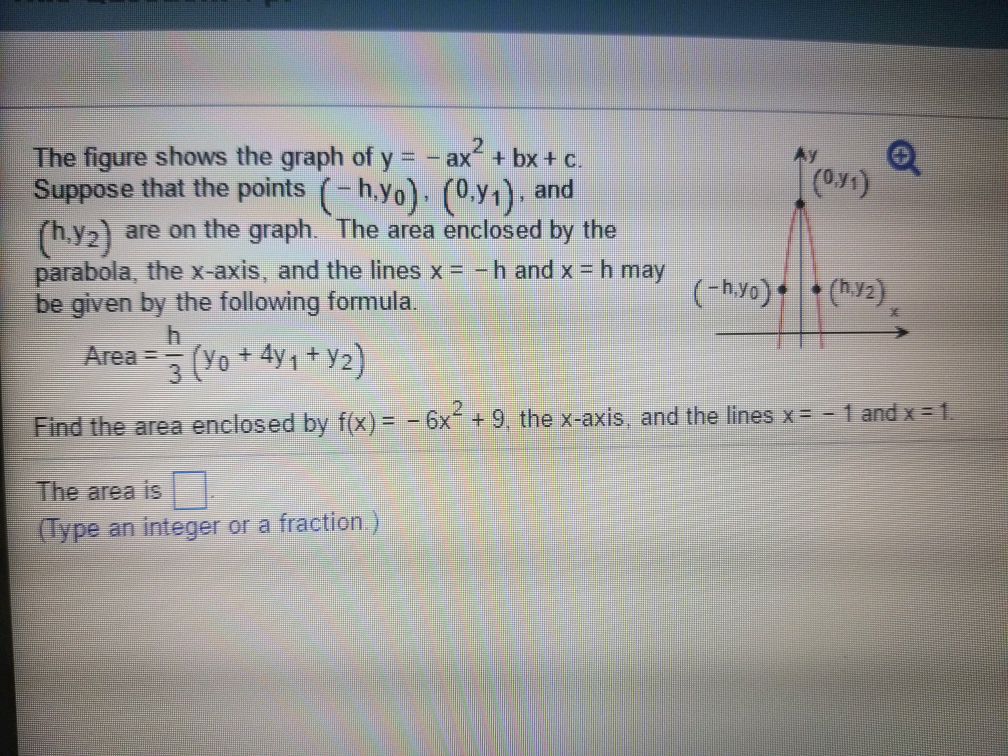
The Figure Shows The Graph Of Y Ax 2 Bx C Chegg Com

Quadratics

Parabola Y Ax 2 Worksheet With Solutions Teaching Resources

Find The Parabola Of The Form Y Ax 2 B Which Best Fits The Points 1 0 4 4 5 8 Mathematics Stack Exchange

Modelli Algebrici Geometrici

Quadratic Graph Example Y Ax Expii

Quadratics

Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube

Axis Of Symmetry Parabola

Chapter 4 Quadratic Functions And Various Nonlinear Topics

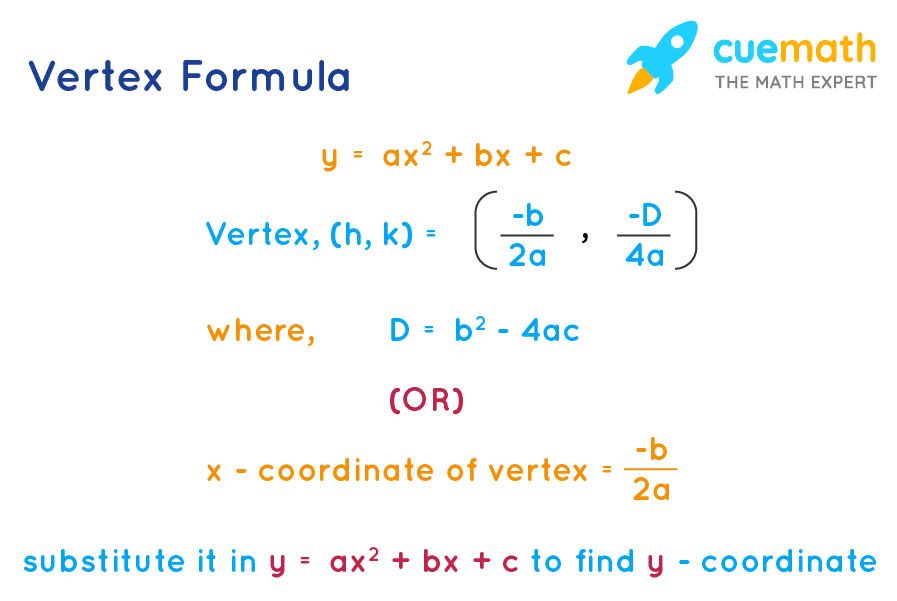
Vertex Formula What Is Vertex Formula Examples

Mfg Graphing Parabolas

Polynomials

Lessons 5

1

Axis Of Symmetry Of A Parabola

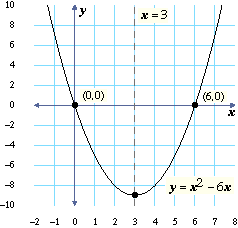
Investigating Y Ax 2 Bx

1

Review

Unique Quadratic Equation In The Form Y Ax 2 Bx C

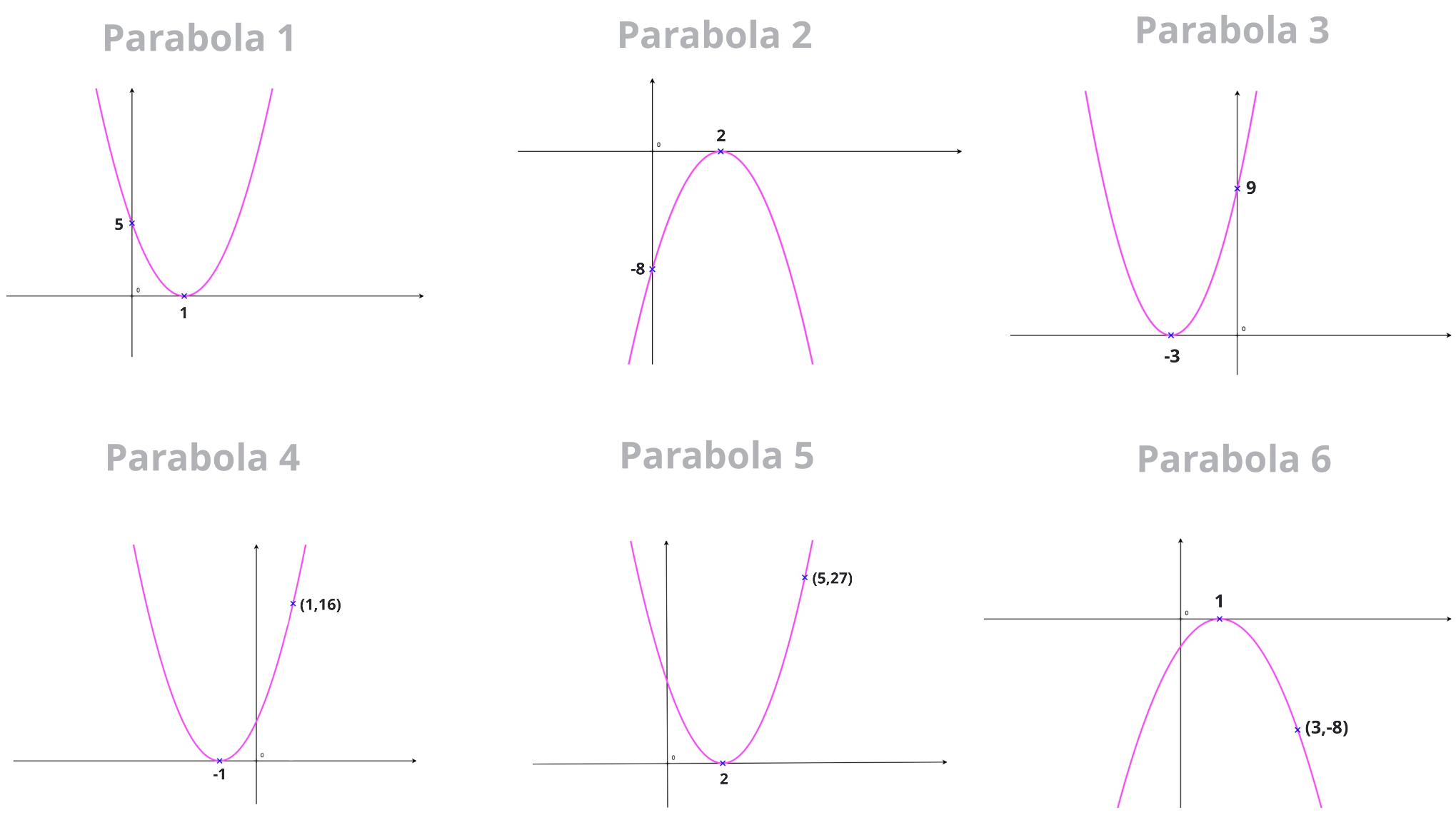
Root Factoring Quadratics How To Find The Equation Of A Parabola

Quadratic Function

Polynomial Functions Quadratic Functions Sparknotes

Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph

Quadratic Formula Calculator

Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Flip Ebook Pages 1 5 Anyflip Anyflip

Quadratic Function

Finding The Y Intercepts Of A Parabola

Graphing Quadratic Functions Quadratic Functions Have The Form Y Ax 2 Bx C When We Graph Them They Make A Parabola Ppt Download

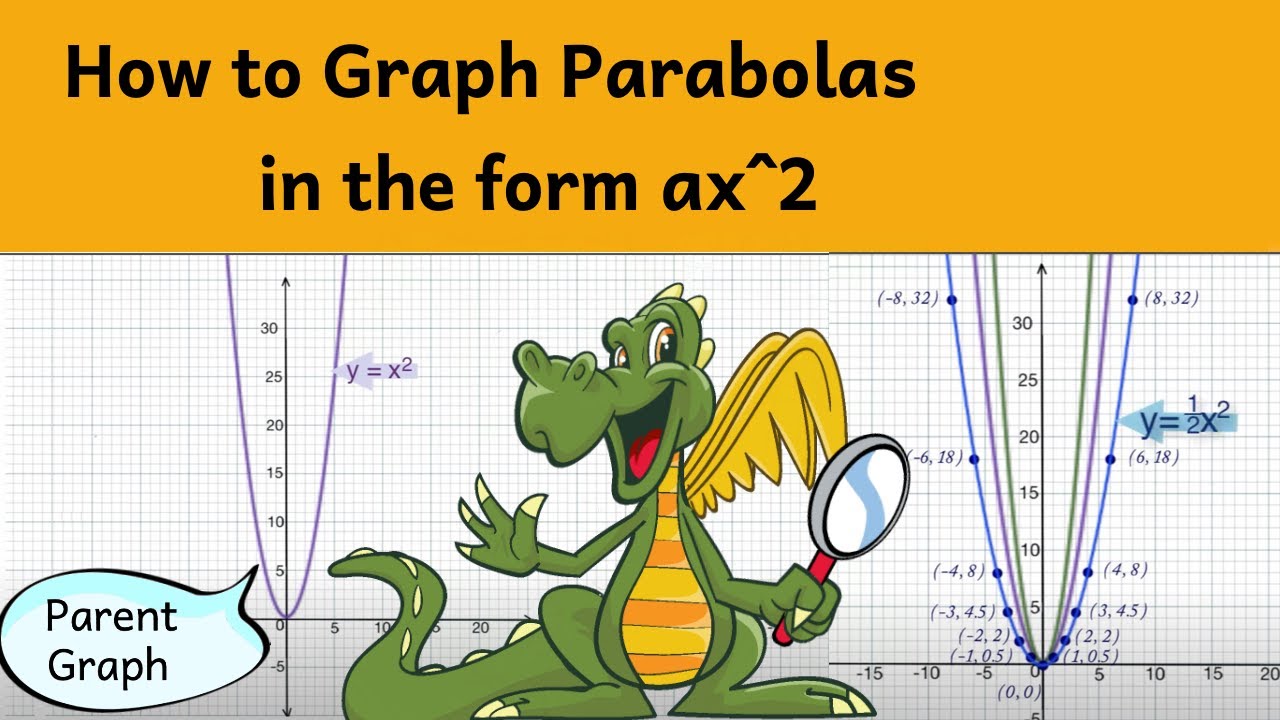
Graphing Parabolas In The Form Y Ax 2 Youtube

How To Find The Vertex Of A Quadratic Equation Video Lesson Transcript Study Com

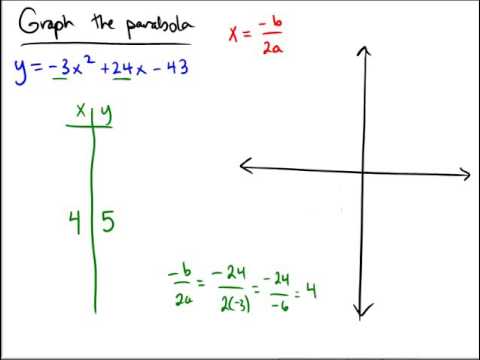
Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube

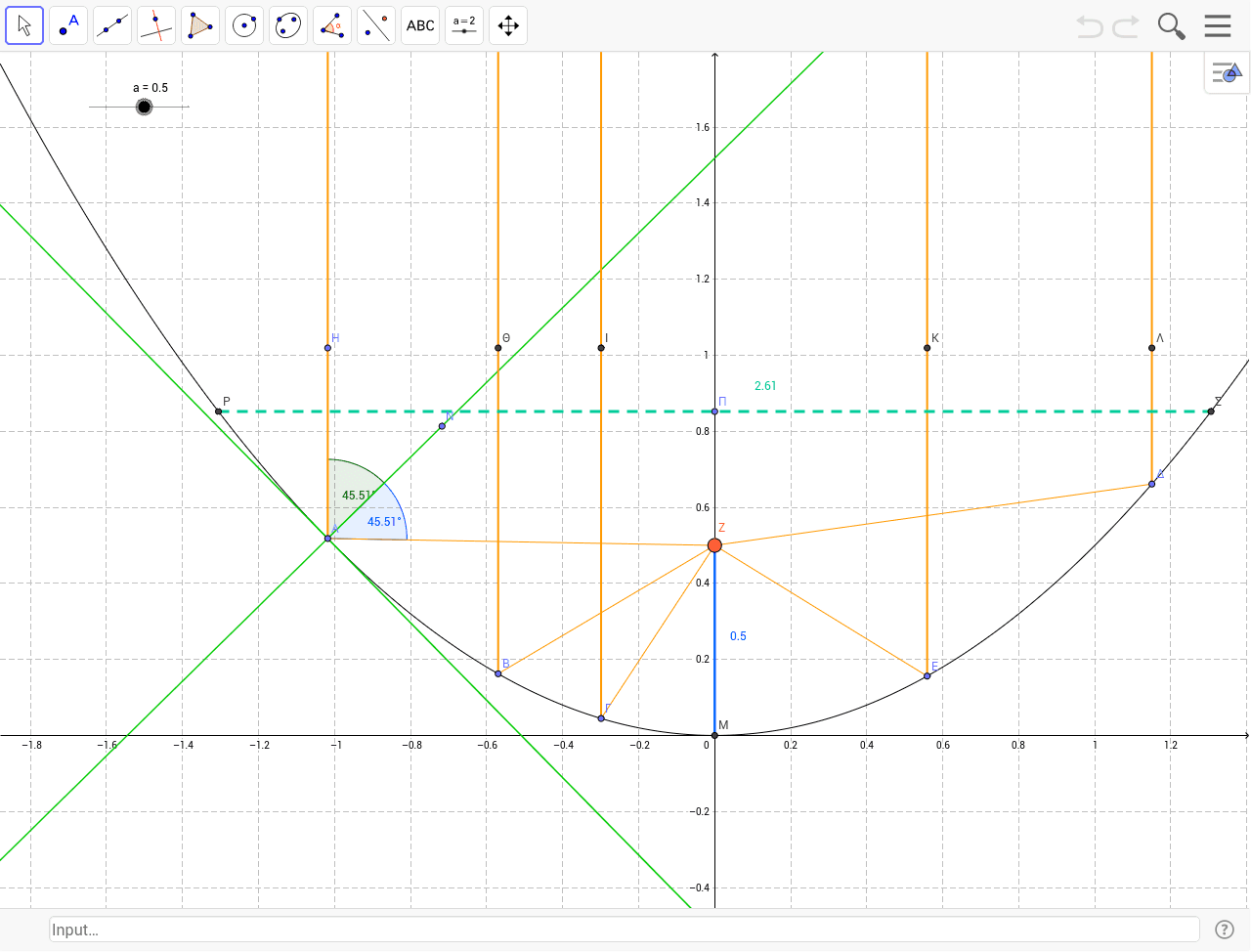
Parabola Y Ax 2 Geogebra

The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora

A Tangent To A Quadratic

Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola

How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora

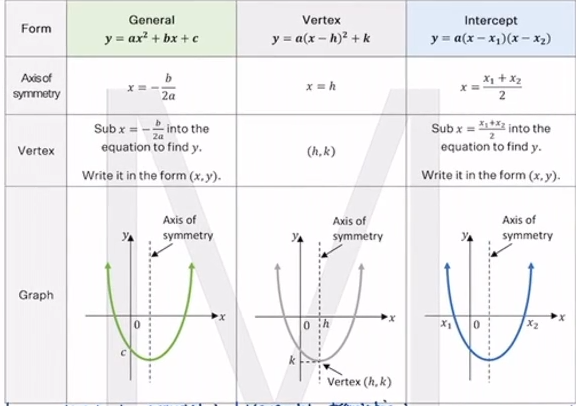
In A Nutshell Parabola Forms Adrian S Study Club

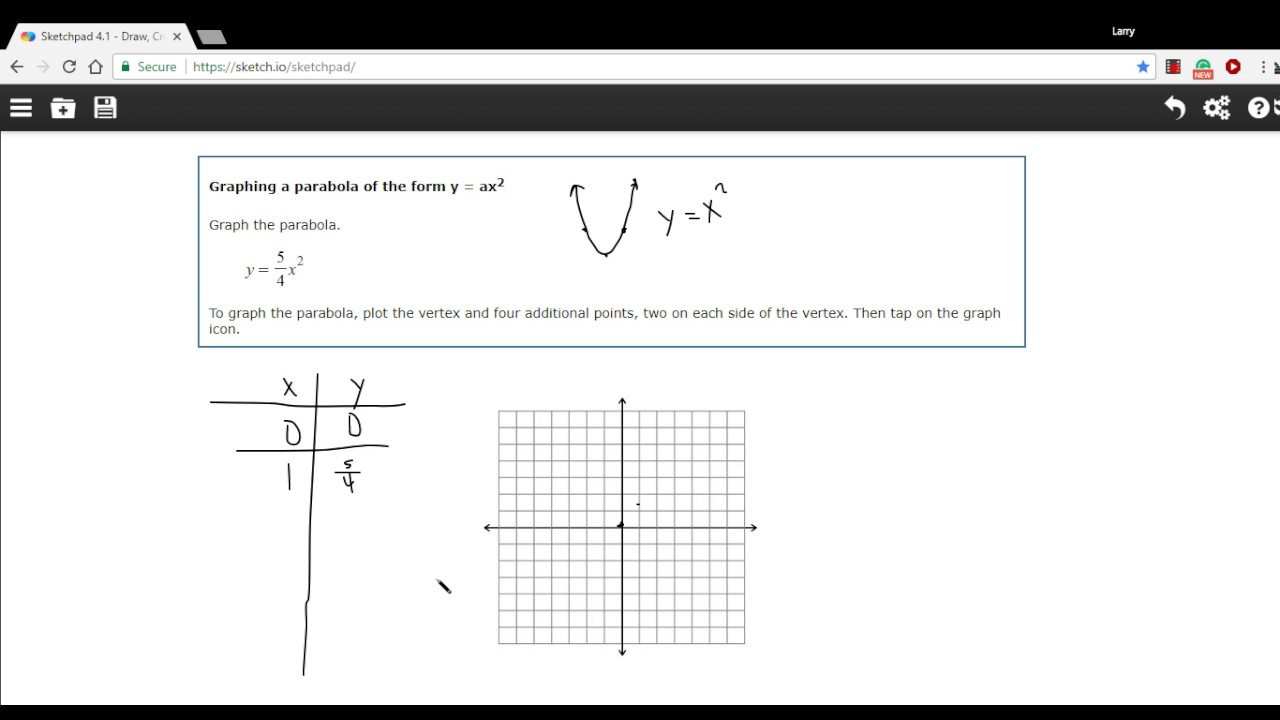
Graphing A Parabola In The Form Of Y Ax Squared Youtube

Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download

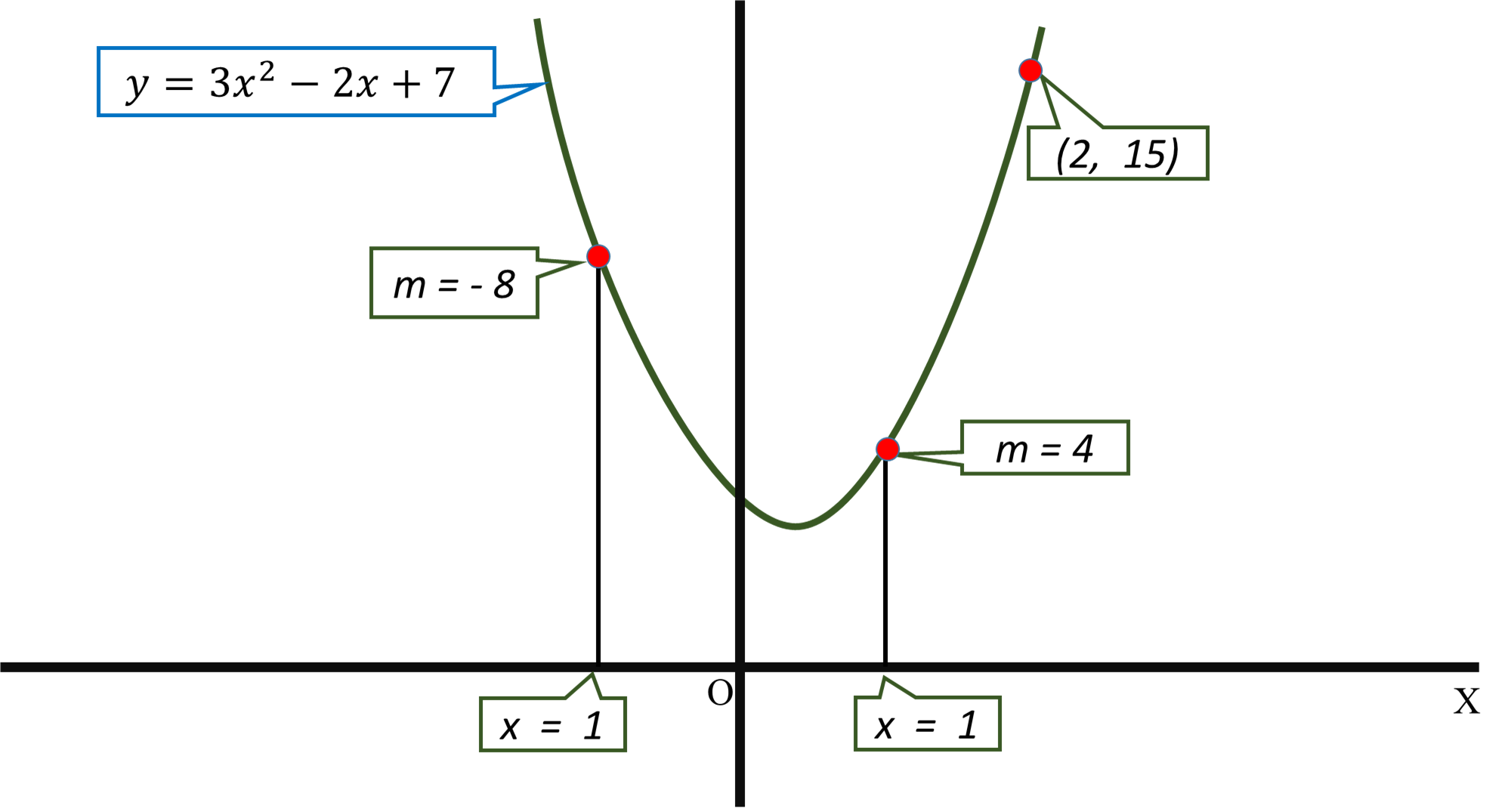
How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic

Quadratic Function

Examining The Parabola Assignment 2

Quadratic Graph Example Y Ax C Expii

Examining The Parabola Assignment 2

Graphing A Parabola Of The Form Y Ax 2 Bx C With Integer Coefficients Practice Study Com

6 3 Quadratic Functions Functions Siyavula

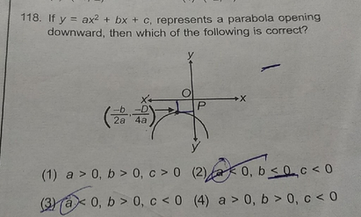
118 If Y Ax2 Bx C Represents A Parabola Opening Downward Scholr

The Function F X Y And Associated Matrices E And E

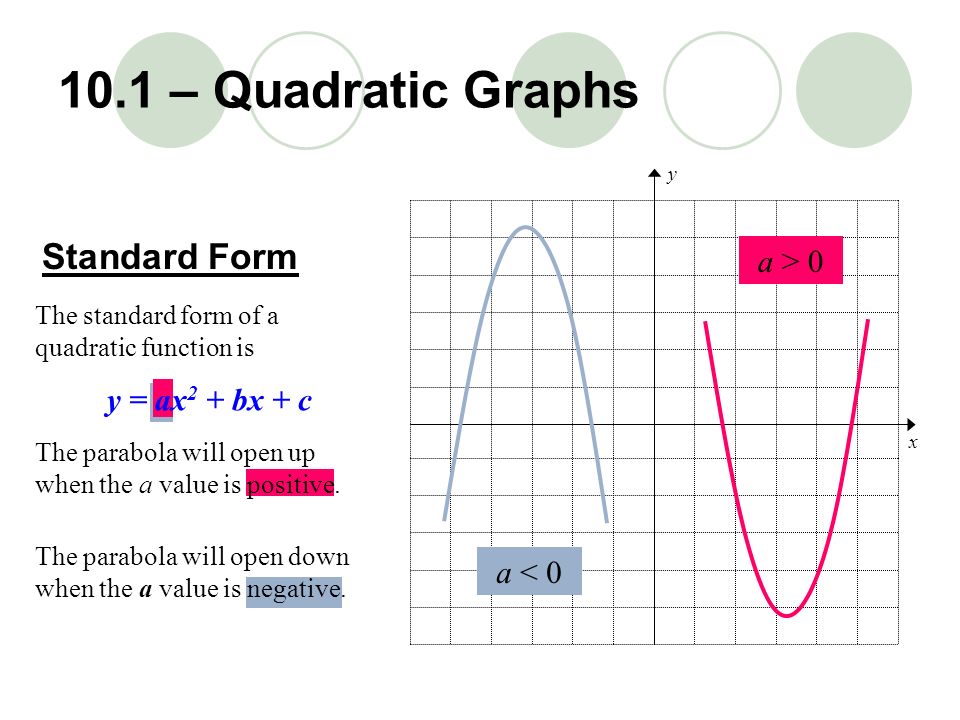
10 1 Quadratic Graphs Ppt Download

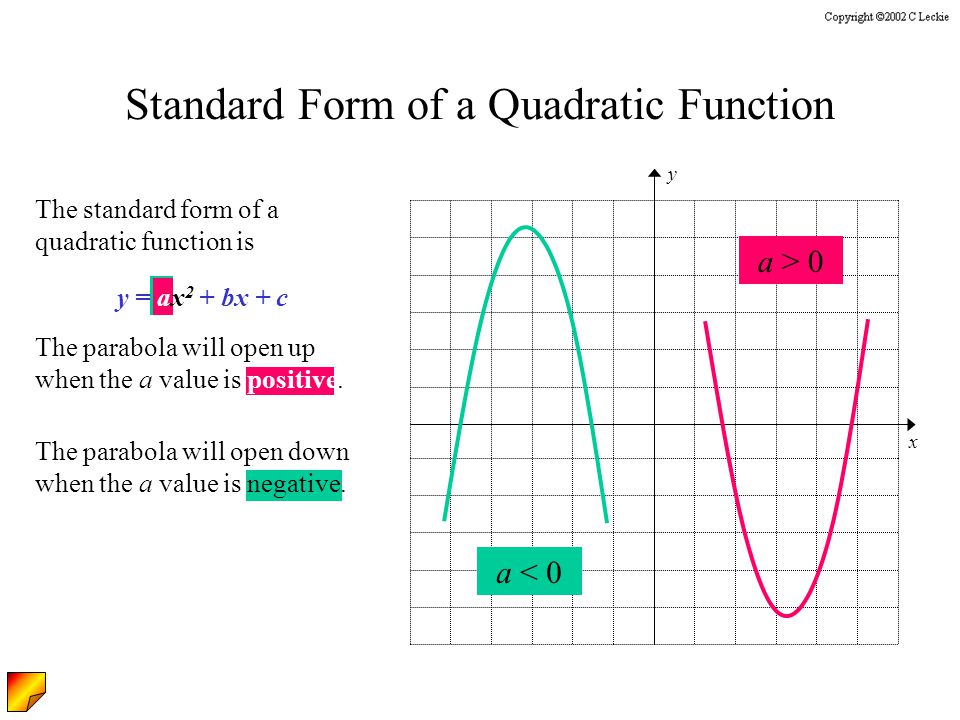
Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download

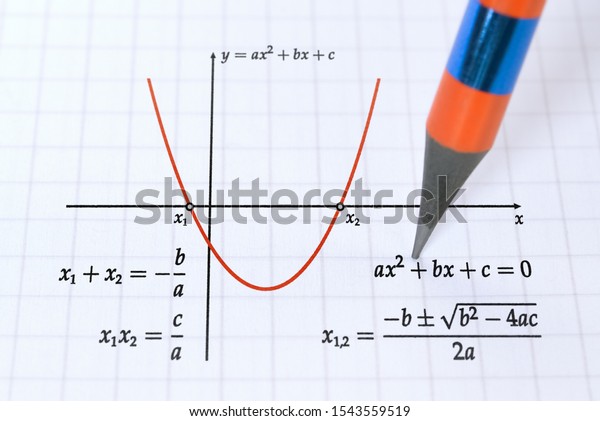
Graph Parabola Quadratic Function Roots Solution Stock Photo Edit Now

Solved Equation Parabola Y Ax 2 Bx C Use Loop Statements Program Capable Finding Maximum Minimum Q

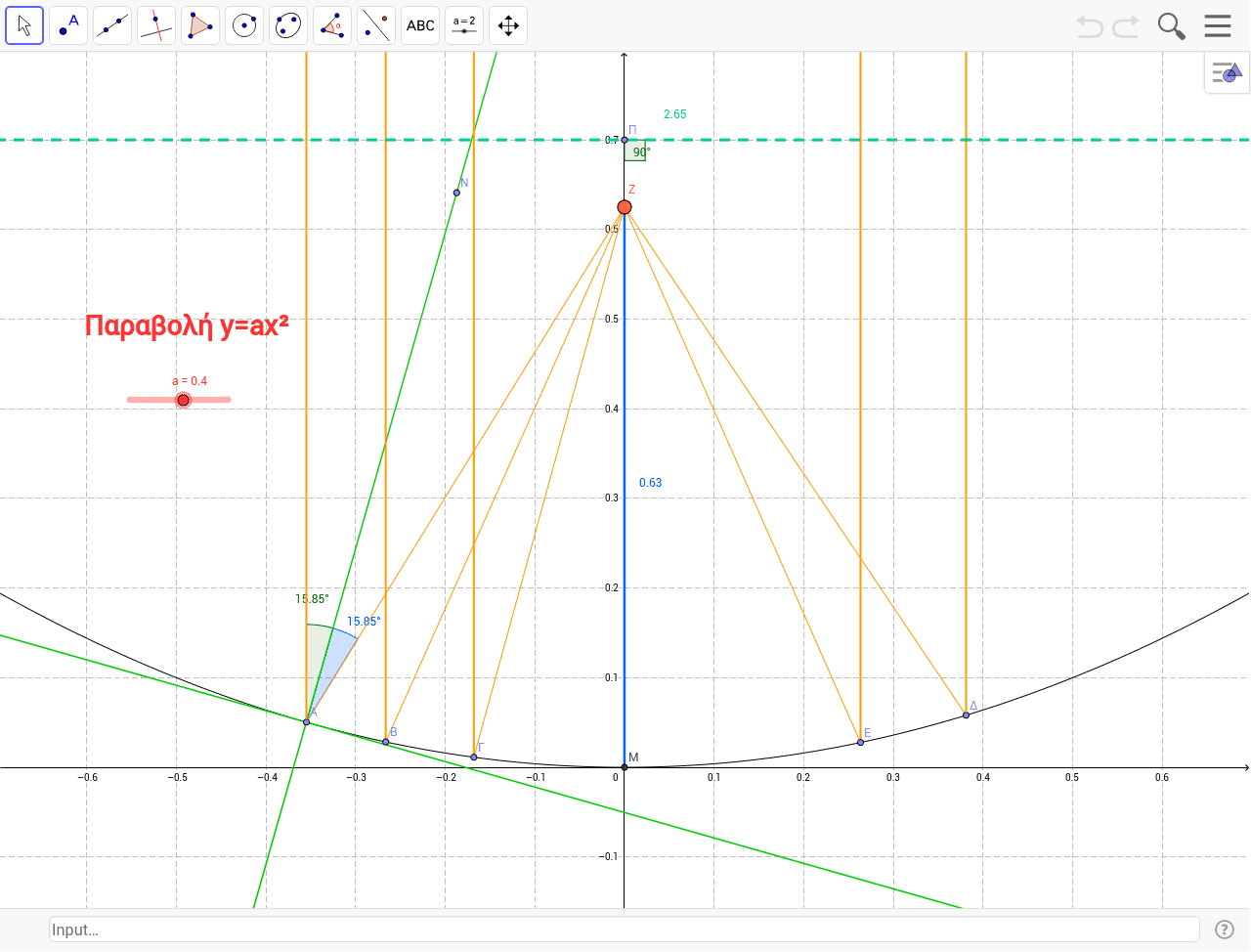
Parabola Y Ax 2 Geogebra

The Graph Of Y Ax2 Bx C Is A Parabola That Opens U Gauthmath

Quadratic Functions Aiming High Teacher Network

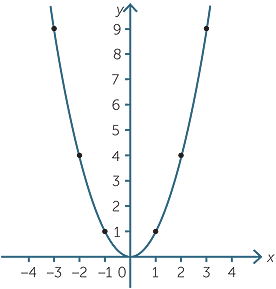
Quadratic Function

Transformations Of Equations Of Parabola Parametric Equations Of Parabola

Quadratics

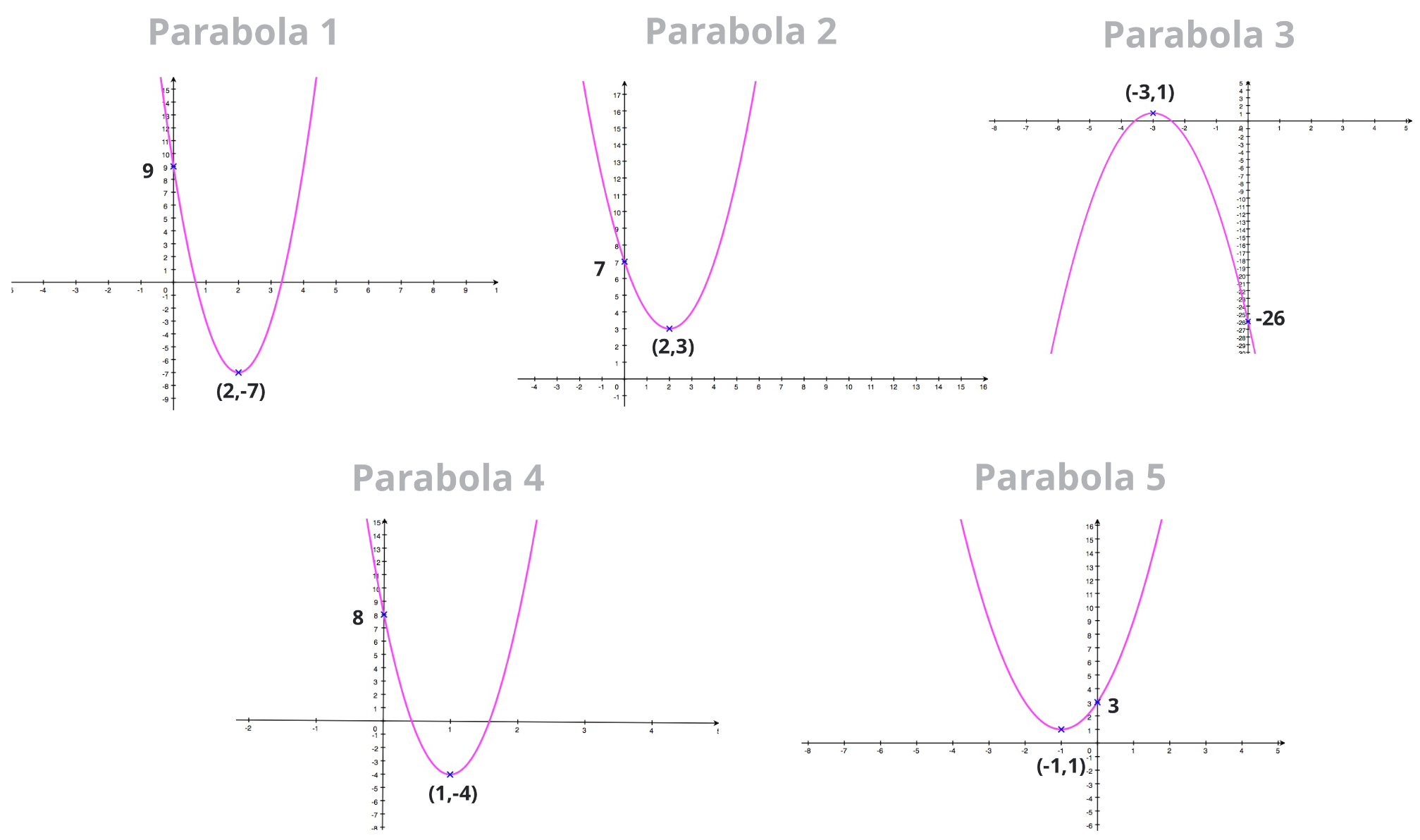
Vertex Form How To Find The Equation Of A Parabola

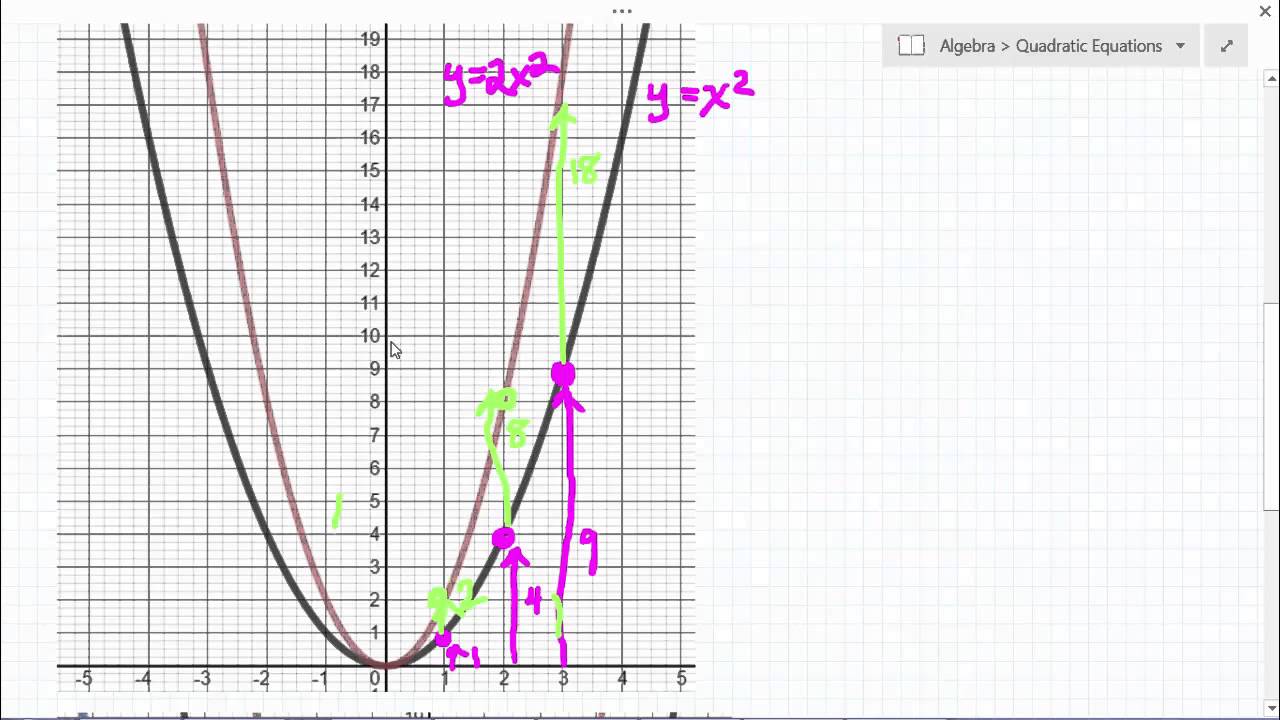
Graphing Parabola Y Ax 2 Youtube

Parabolas

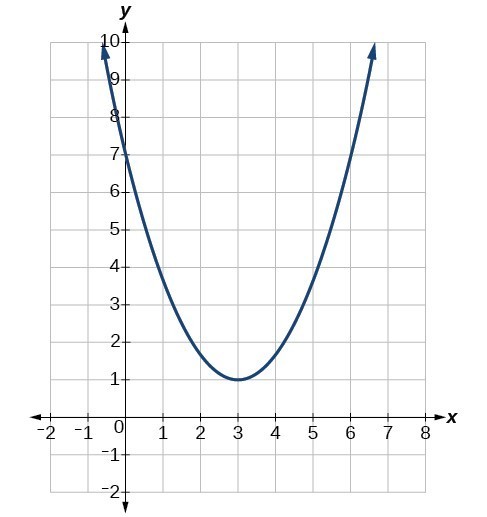
Characteristics Of Parabolas College Algebra

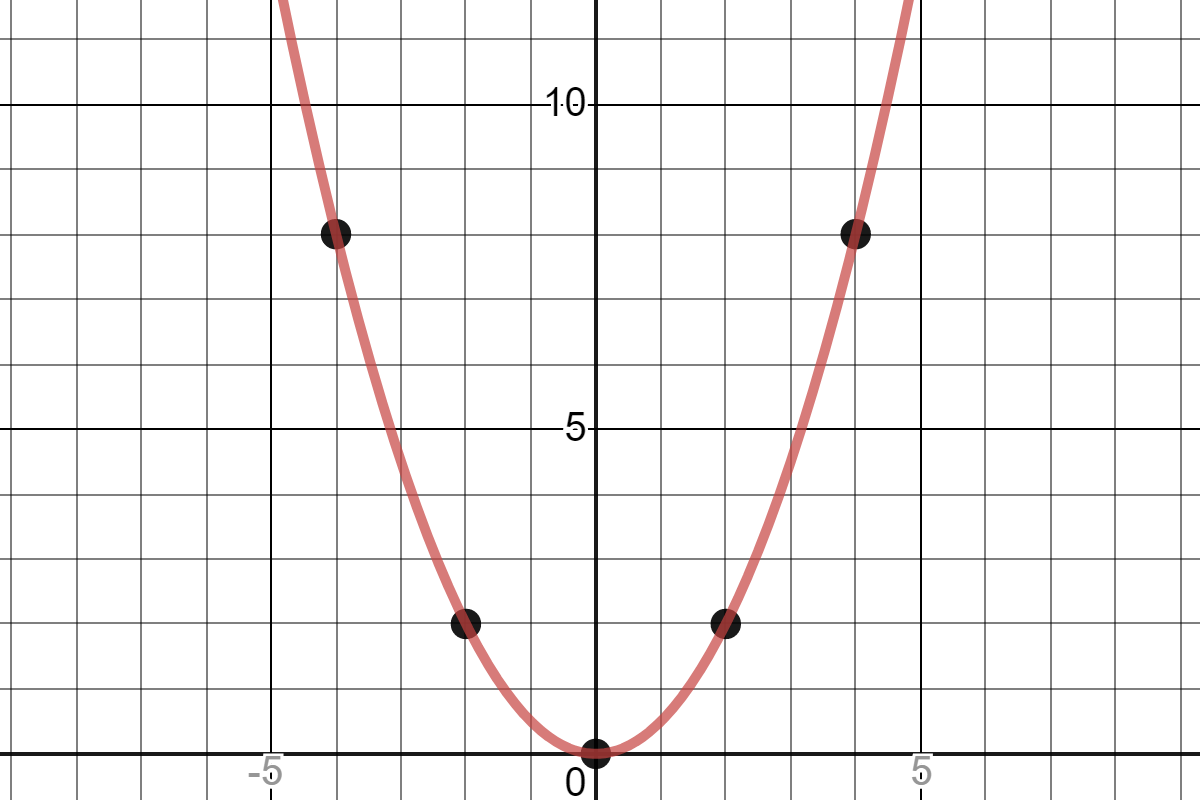
Quadratic Graph Example Y Ax Expii

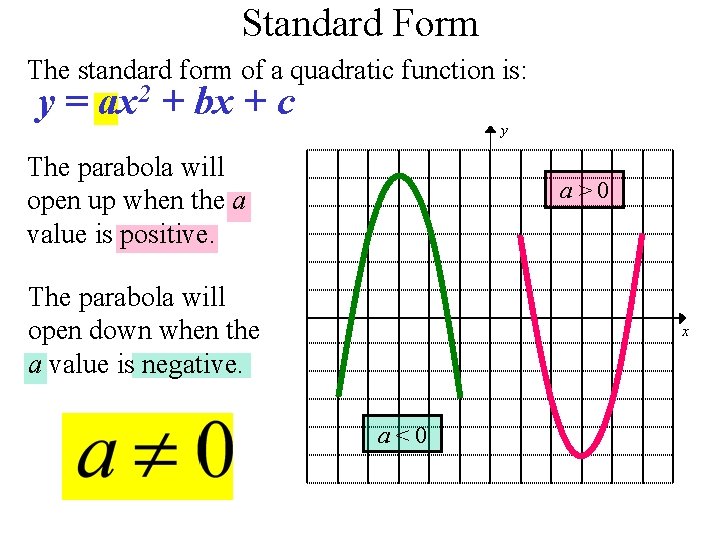
Quadratic Function Y Ax 2 Bx C Quadratic

Incoming Term: y ax 2 parabola open, y ax 2 bx c parabola, parabola y ax 2,