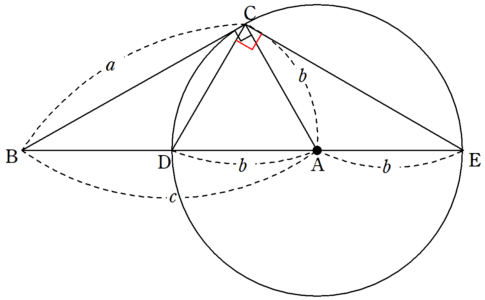
合同条件と相似条件の似ているところと、違うところを中心に復習していくよ。 三角形の合同条件と相似条件を3つの種類にまとめてみた 三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。 3つの何かが等しい条件傍接円、傍心について 中学生へ 三角形の外角の二等分線の交点を「傍心ほ(ぼ)うしん」といい、傍心は全部で3つあり、下の図で ABCの傍心は点P、Q、R の3つです。 1990年ごろの中学の教科書にも傍心という用語は出てきませんが、傍接円と接線の長さ それでは,すべての放物線が相似であることを証明しよう。 証明 放物線 C のグラフを原点を相似の中心として, a b ( > 0) 倍にしたグラフ D も放物線であることを証明する。 放物線 C 上の点 A ( x, y) の移動後の点を A ′ ( X, Y) とすると, O A ′ → = a b
Studydoctor相似の位置と中心 中3数学 Studydoctor
相似の中心 証明
相似の中心 証明- 三角形の相似条件 中3数学 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99%「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。相似であることを証明するには「2組」を示せば十分だということ 右図では ∠B=∠Q, ∠C=∠R を示せば, ∠A=∠P は自動的に成り立つ. (2) 「3組の辺の比がそれぞれ等しい」という書き方は2種類ある.
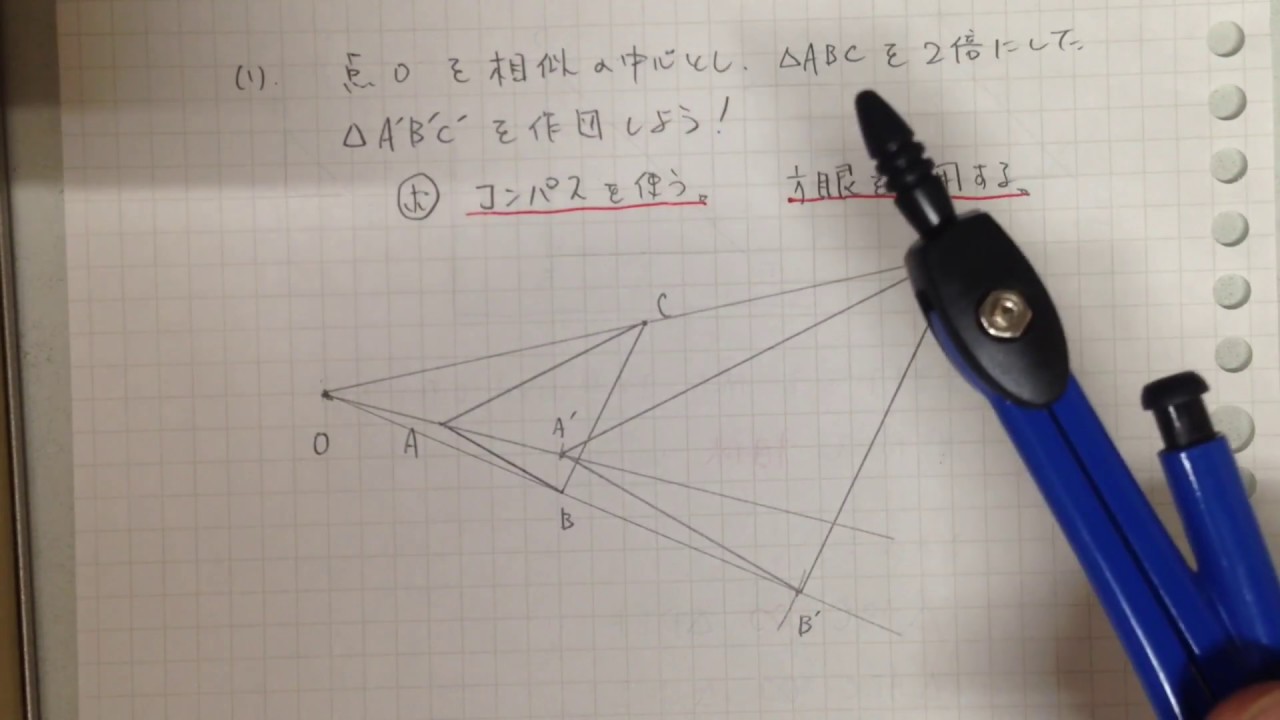



中3 数学 相似 2 作図しよう Youtube
円周角と図形の証明 1 次の図のように、円Oの2つの弦AC、BDの交点をEとするとき、以下の問いに 答えなさい。 (1) ABE DCEであることを証明しなさい。 365 B A D C E o 2 次の図のように、円Oの円周上に4点A、B、C、Dがある。BC=CDであるとき、2 相似な図形の性質や相似比について理解させる。 イ-① エ-① 3 相似比を利用して,対応する辺の長さを求めることができるようにする。 ウ-② 4 拡大図のかき方を通して,三角形の相似条件を理解させる。 イ-② ウ-③ エ-② 5・相似の位置や相似の中心を理 解し,相似な図形の性質,相 似比について理解する。 (1) ・相似な図形の性質を理解して いる。 ワークシート 自己評価表 単元の目標 指導と評価の計画
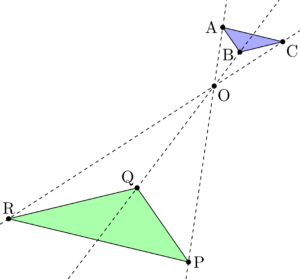
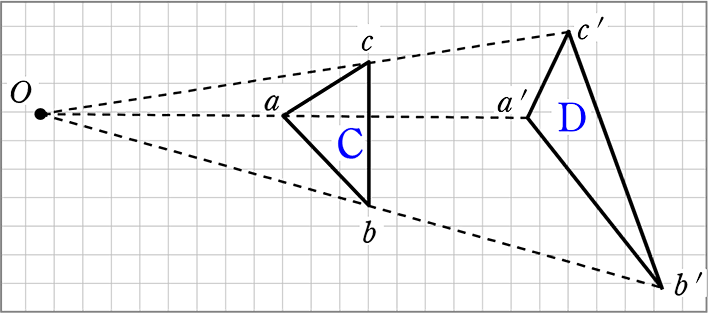
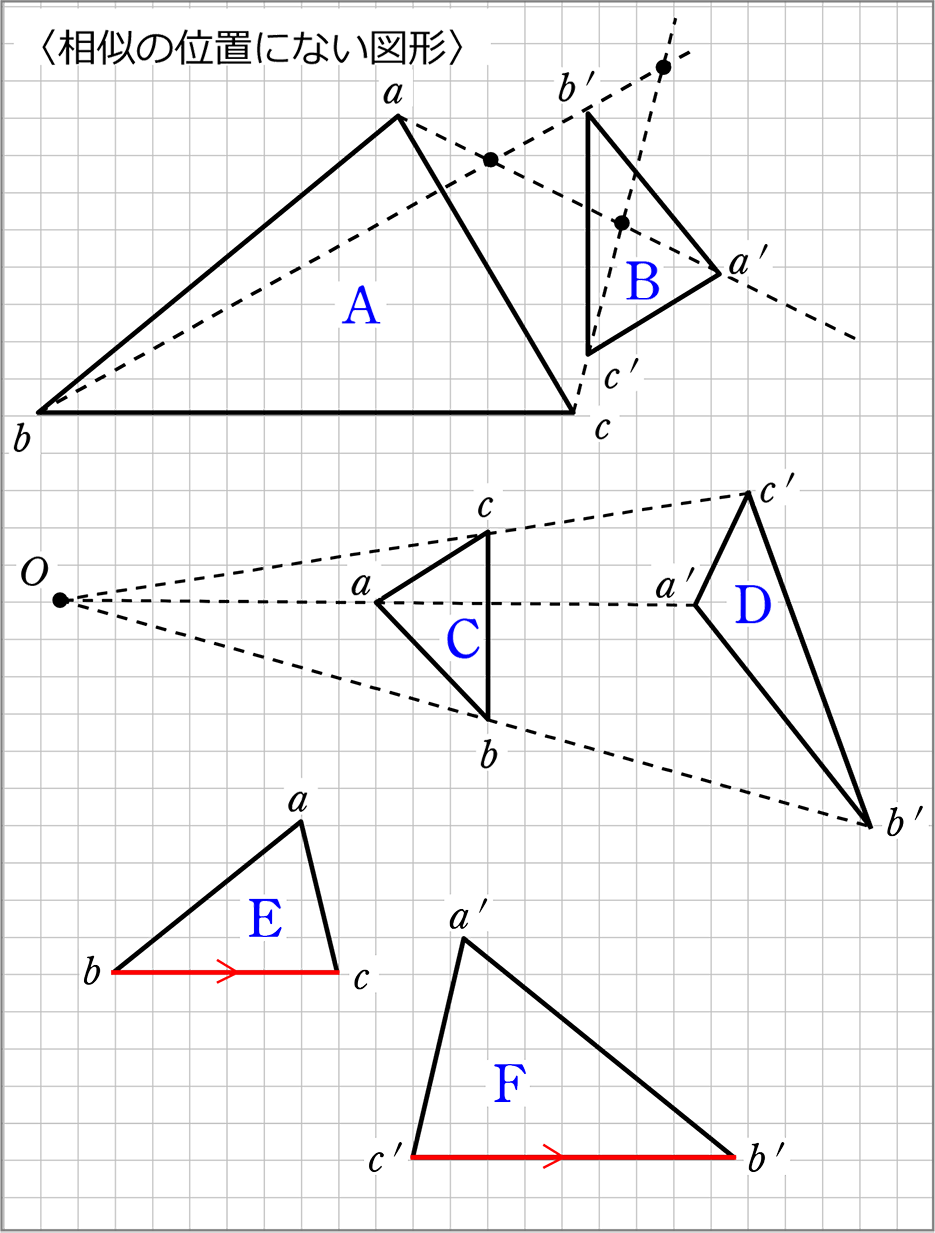
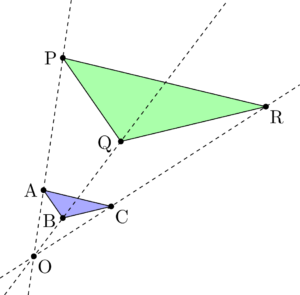
4-8.平面図形 相似の証明 複合問題ほか 11年度出題 問1 図のように,辺acが共通な2つの二等辺三角形abcとacdがあり,ab=ac=adとします。∠acbの二等分線 と辺daの延長との交点をeとし,辺abとceとの交点をfとします。次の問いに答えなさい。上の図で、外接四角形の極線の上にKがあることを証明する。 ただし、MOの極をKとする。 KがHG上にあることは明白。 さらにIの極線とHGが一致することも明白。 最初に証明したことから、対応する接点と対角線が一点I(極)で交わる。Pとaとa'の3点を通る円、pとbとb'の3点を通る円を描く。この2つの円の交点oが不動点になる。図2が作図の例であるが、 oabと oa'b'が相似の関係になっていてoを中心に縮小させながら回転すると辺abが辺a'b'に移動することが理解できるであろう 。 その2
当然「相似の中心O」もありませんね → 「相似の位置」にあるかないかは、点線を引かなくても、 対応する辺がそれぞれ 平行か平行でないか 、パット見でわかりますね! ex) 辺abと辺a'b'を見比べて平行でない!→相似の位置にない!22 学校数学における相似の定義と相似な図形の性質 小学校6 年生では,中学校で学習する素地として,拡大と縮小を学習する.小学校の教 科書では,いろいろな縦と横の比の図を見せ,形が同じで大きさが違う図形について考え〇なぜ相似になるかを根拠 を明らかにして説明する 活動。 〇相似条件が成り立つ理由 を考える活動。 4 三角形の相似条件と証明 (2 時間) A 〈目標〉 図形の中から相似な三角形を見いだし,三角形の相似を証 明することができる。 問題



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor



中学数学 図形の相似
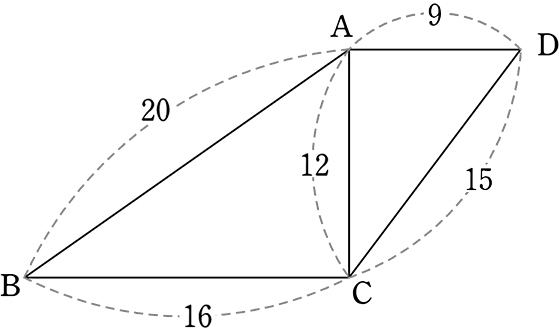
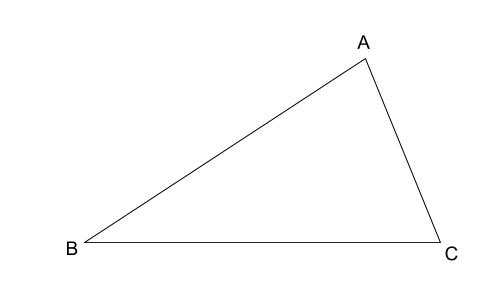
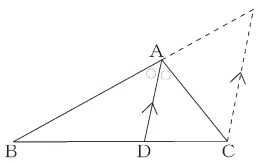
て考察する。相似の中心を任意に取り、作図する方法 を理解する。 縮図や拡大図を見付けたり、生活に生かしたりする活動を通して、拡 大図と縮図を日常に生かしていこうとする態度を育てる。 〇学習内容の定着を確認し、理解を確実にす る。この3つの中から相似な図形を見つけるときに 情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている ABCと ABDが相似になるだろうな、と予想して この2つの三角形が、相似条件に当てはまるかを確かめていきます動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



中学数学 図形の相似



三平方の定理の証明 相似を利用した証明3 Fukusukeの数学めも
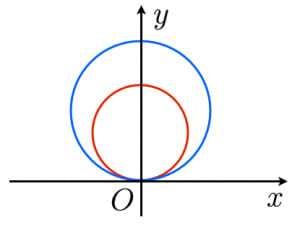
3年生の相似条件と証明についてです! 2年生のときに習った合同条件とは違うところを簡単にまとめてみました☺︎ 見辛いかもしれません🙏 学年 中学3年生, 単元 相似な図形, キーワード 相似条件,証明少し知識が必要であるが,シムソンの定理を援用して証明する。 2 変換幾何による方法 (a) 三角形の相似を使う2方法 補助線を使って,二組の相似三角形を作り,相似比から結論を導く。簡潔で,非常に美 しい証明。 (b) (射影変換の)複比を使う方法 放物線が相似であることの証明 y = a x 2 b x c y=ax^2bxc y = a x 2 b x c のグラフとして表される放物線たちは,強い意味で,すなわち回転を許容しない相似です。 任意の2つの放物線に対して相似の中心が存在して,一方は他方の拡大(縮小)になっています。



Mathematics 相似 1 相似の定義 定理とその証明 働きアリ The 2nd
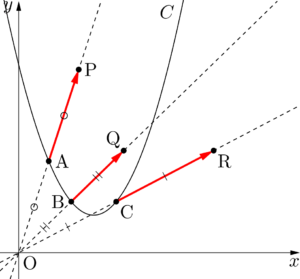



すべての放物線が相似であることの証明 ページ 2 大学入試数学の考え方と解法
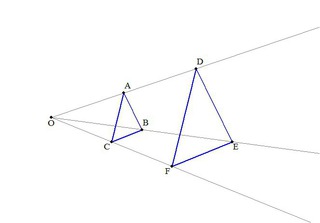
円周角 円と相似1 名前 右の図のように2つの弦ac,bdの交点をp とする。 ①papd=pbpcとなることを 証明しなさい。『相似な図形 相似な図形の証明』 J—3 レポート ア、円周角と中心角の関係の意味を理解し、それが証明することができることを知る。 イ、円周角と中心角の関係を具体的な場面で活用すること。 (2)観察、操作や実験などの活動を通して、三平方の定理相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 図形は,o を相似の中心として相似の位置にあるという。




これらの相似の証明の仕方が分かりません 解き方を教えてください 出来れば 相似の証明 Clear
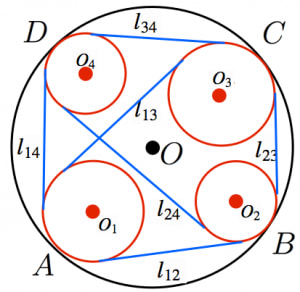



ケージーの定理とその証明 高校数学の美しい物語
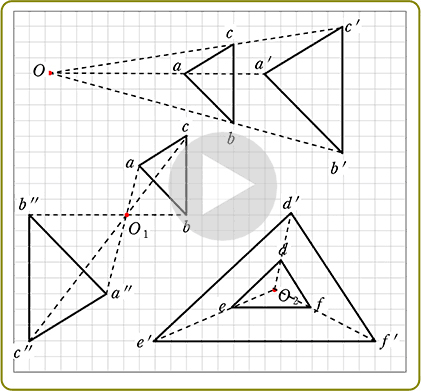
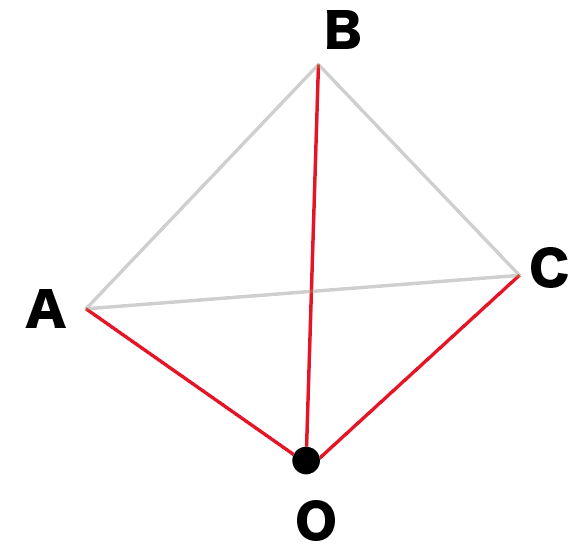
相似の中心o が三角形の内部にあるときも同様である。 下の図は,点o を中心として,4abc を3 倍に拡大した 4def をかいたもので,どちらの場合でも4abc と4def は相似の位置にある。 a d e f b c o a d e f b c o oa od,ob oe,oc of がどれも1 3 になっている ことを確かめよう。相似の基礎 相似(そうじ) は日本語で、「一方の形や性質が他方のそれを丸写ししたように、互いに似ていること」という意味になりますが、数学では、「 1 1 つの図形を均等に拡大または縮小して他と完全に重なる状態( = = 合同)のこと」をいいます~ 図形 ・三角形の相似条件の理解 形を証明したり、図形の性質・相似の中心、相似の位置の意味 8時 ・ 相似比 を求め た り 、利説明 しする力 知 それ 用 て拡大図 ・ ・ ~ ~



Studydoctor相似の証明の基本その2 中3数学 Studydoctor



平面の変換
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは次に,i点oが相似回転の中心である」ことを証明する。すなわち,ムaoe,ムbof とムcogが相似であるこどを示す。 6aoeとムbofにおいて, (5) より bo oa bo fo ー'一fo oe oa oe' また,ムabo∞ムefoよりどaob=どeofだから,・ (8) laoe=どaobleob 中3数学図形と相似相似な図形と証明(1~9)のプリント集です。 相似な図形 相似な図形の性質を用いて角度の大きさや線分の長さを求める 三角形の相似条件 相似な図形の証明 相似な図形の証明の応用問題 問題・解答解説付きです。



相似の中心と作図 Youtube



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 3nen2 02 Pdf
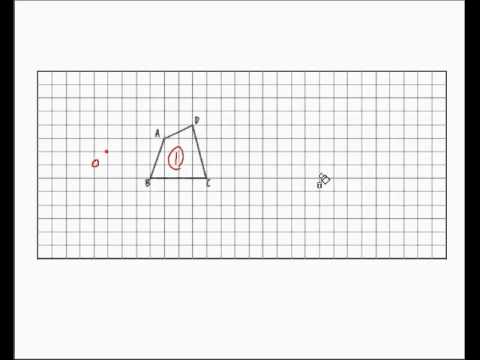
相似比 相似な図形で、対応する線分の長さの比を相似比(そうじひ)といいます。 三角形の相似条件 2年生では三角形が合同になる条件を考えました。ここでは三角形が相似になる条件を考えてみましょう。 三角形の相似条件は、次のようになる。また, そのときに使った相似条件を答えなさい。 ⑴ d⑵ 3 右の図のように, abc の頂点a から辺bc に垂線ad をひき, d さらに点 から辺ac に垂線de をひきます。この図の中から, 相似な三角形を答えなさい。また, そのことを証明しなさい。数学35章図形と相似「相似な図形」<応用問題> 組 番 名前 1次の図のように,平行四辺形ABCDを点Cを中心に 時計回りに回転させ,点Dが辺BCの延長上の点Gにく るようにすると,2点A,Bは,それぞれ点E,Fに移 動しました。 証明しなさい。



相似な図形 Banshot



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su




相似の証明と面積の計算 abcでaから辺bcにひいた垂線をad 外接円 Okwave



平面の変換



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



Studydoctor相似の位置と中心 中3数学 Studydoctor




円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方



学習指導要領ナビ Jp 中学校 数学 第3学年の内容 b図形 図形の相似




動画で学習 3 相似の位置 数学



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



高校入試 英語 数学 図形と相似 相似の基礎



Http Www Kumamoto Kmm Ed Jp Sugakubraindumps Pdf 3 5 Answer Pdf




相似な図形 相似な図形 1 を教えてください Clear



相似の中心と作図 Youtube




三角形の相似条件と証明問題の解き方 数学fun



すべての放物線が相似であることの証明 大学入試数学の考え方と解法



1



平面の変換



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor



中学数学 図形の相似




3 解説見ても分からないんですけど もっと分かりやすい解き方ないですか Clear



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



Http Www2 Gsn Ed Jp Houkoku 03c 03c07 03c08s Pdf



放物線の相似性



Happylilac Net Pdf Jhs Math3 05 01ans Pdf



中3数学相似の中心を使った縮小した図を書く問題があるんですが書き Yahoo 知恵袋



Top



2



高校入試 英語 数学 図形と相似 相似の基礎



1



中学校数学 3年生 図形 相似な図形 Wikibooks



接する2つの円の相似の中心 高校数学の美しい物語




円の相似拡大 縮小 Etc Den Of Hardworking




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット



放物線の相似性



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋
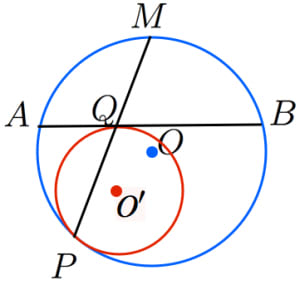



接する2つの円の相似の中心 高校数学の美しい物語



高校入試 英語 数学 図形と相似 相似の基礎
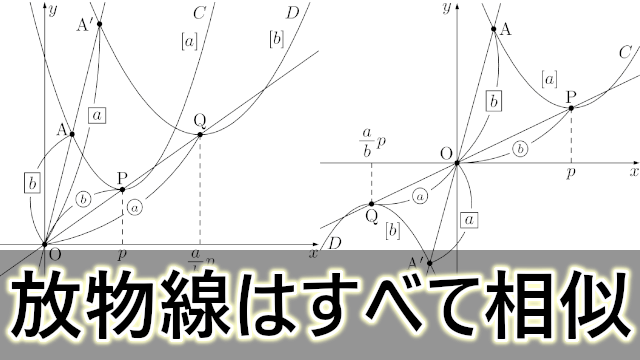



すべての放物線が相似であることの証明 大学入試数学の考え方と解法
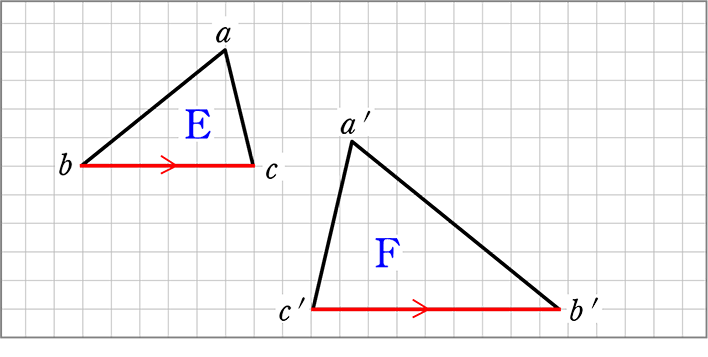



中学数学 図形の相似
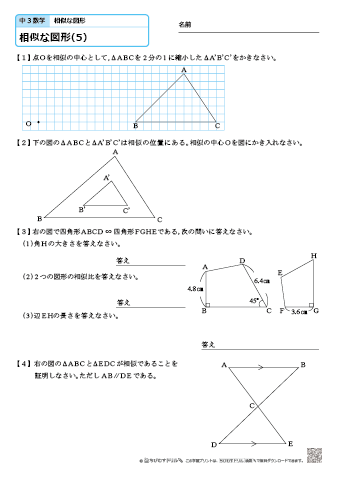



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
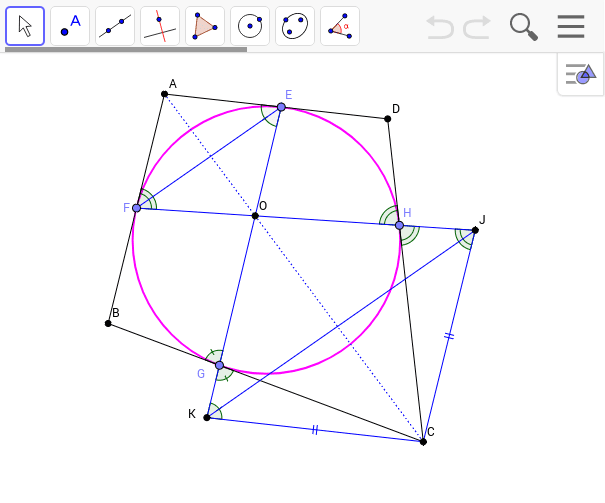



外接四角形の対角線の証明 Geogebra




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files J3 Pdf



中学数学 図形の相似
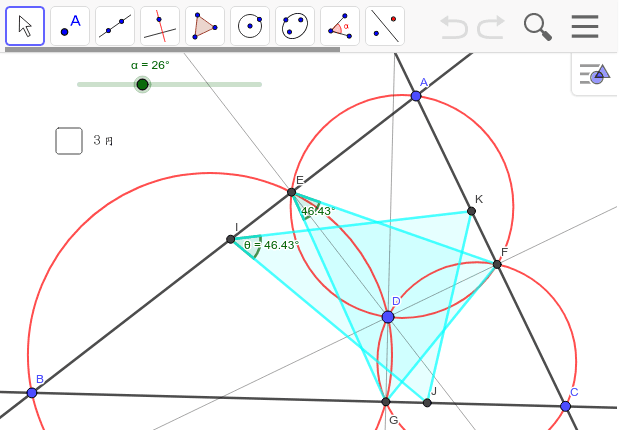



三角形に内接する相似三角形 Geogebra
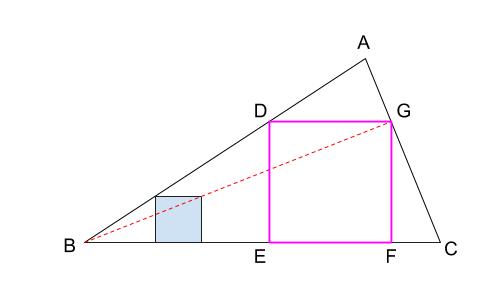



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su




の証明を教えていただきたいです Clear




簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



すべての放物線が相似であることの証明 大学入試数学の考え方と解法
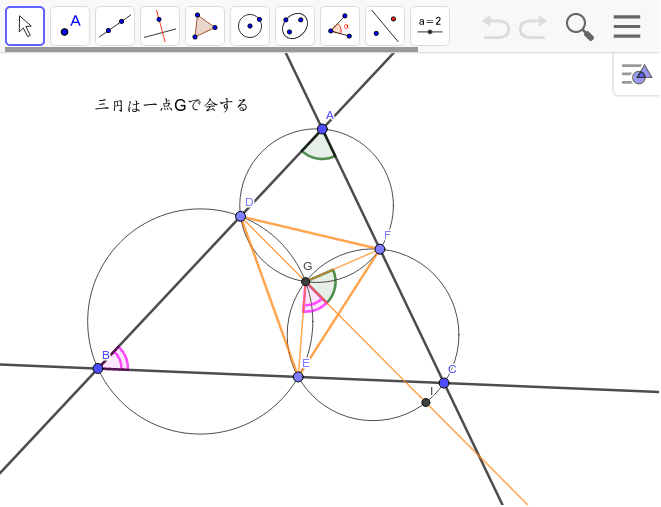



三角形に内接する相似三角形 Geogebra
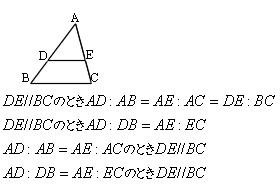



Mathematics 相似 1 相似の定義 定理とその証明 働きアリ



平面の変換
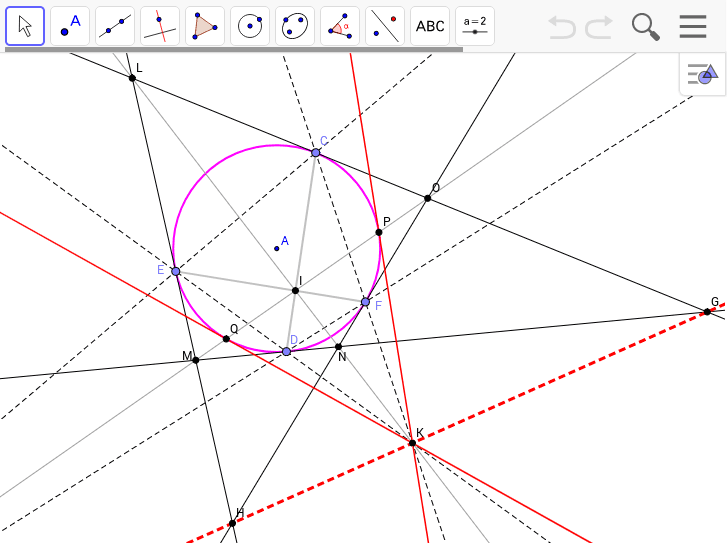



外接四角形の対角線の証明 Geogebra
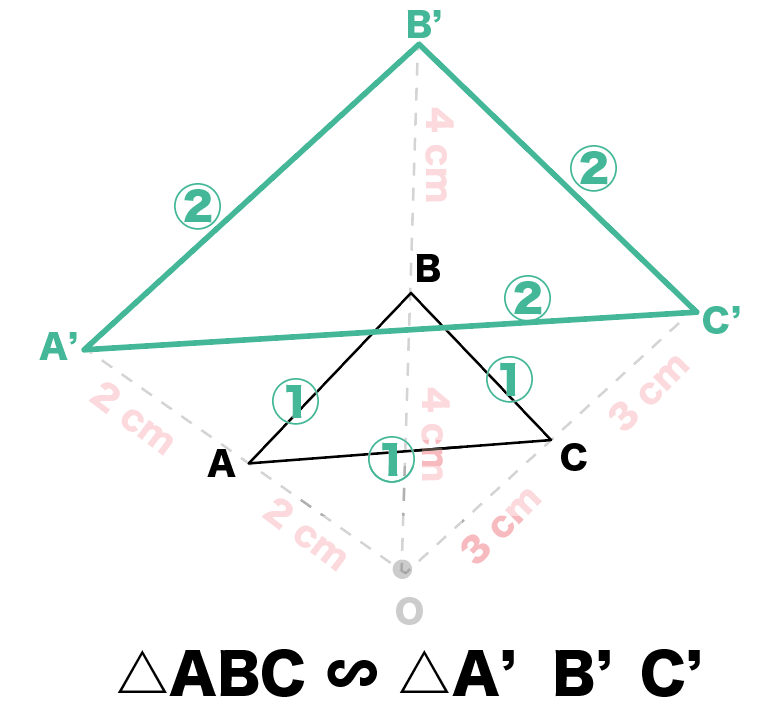



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
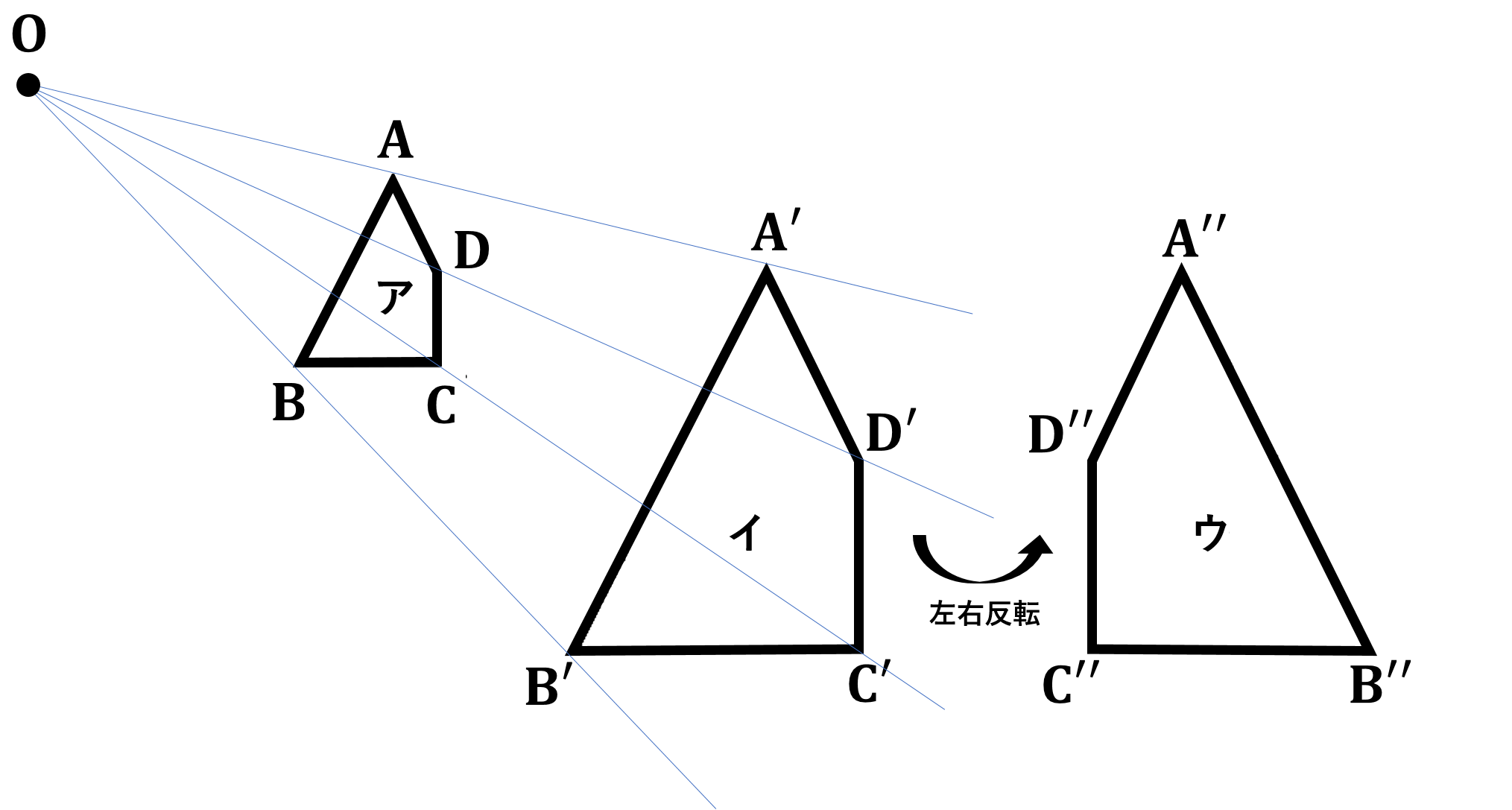



5章 相似 タカラゼミ




相似な図形 相似な図形 1 を教えてください Clear




中3数学 拡大図 縮図の作図 映像授業のtry It トライイット




てなぐさみのメモ 相似の導入のあれこれ6 芳沢 新体系 中学数学の教科書 の場合




B Bar8cm C E Bar10cm G Lihat Cara Penyelesaian Di Qanda
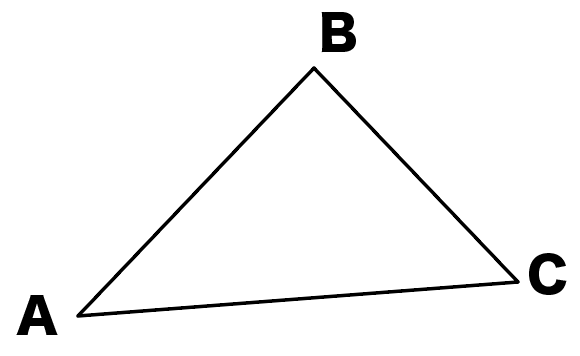



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



四角形a B C E は点oを相似の中心として四角形abcdを2分の Yahoo 知恵袋



高校入試 英語 数学 図形と相似 相似の基礎




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題
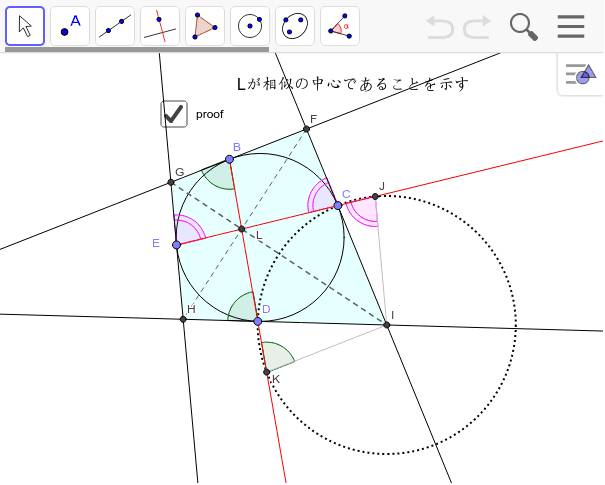



四角形に内接する楕円の作図 Geogebra



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋




中3 数学 相似 2 作図しよう Youtube



B Bar8cm C E Bar10cm G Lihat Cara Penyelesaian Di Qanda




相似の中心と作図 Youtube



Http Www Asahikawa Hkd Ed Jp Asahi Els 13 Seien Suugaku30 Pdf
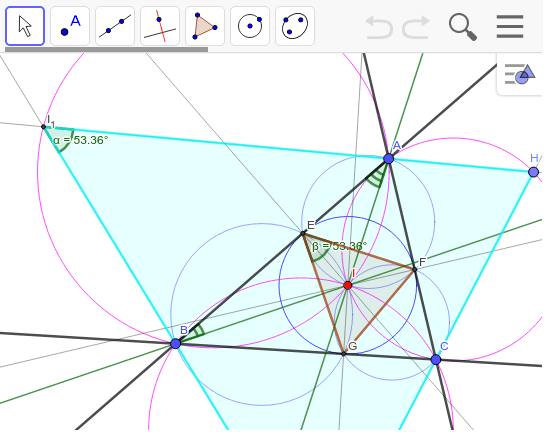



心を中心とする三円 Geogebra




初等数学模索生活 相似な図形 1
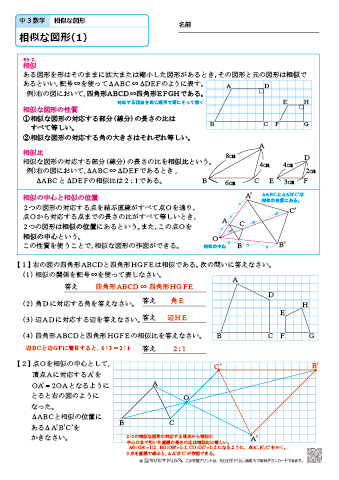



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Www Hiroshima U Ac Jp System Files 910 E6 95 B0 E5 Ad A6amano Pdf



1



平面の変換



1



相似の例題解説 01 相似な図形 操作 目次の項目 をクリックすると 解答画面に行きます Rei1 Jpg 解答画面 拡大縮小の図形シミュレーター Rei011 Jpg 02 相似な図形のかき方 Rei2 Jpg 03 相似な図形のかき方 Rei3 Jpg 04 相似な図形の
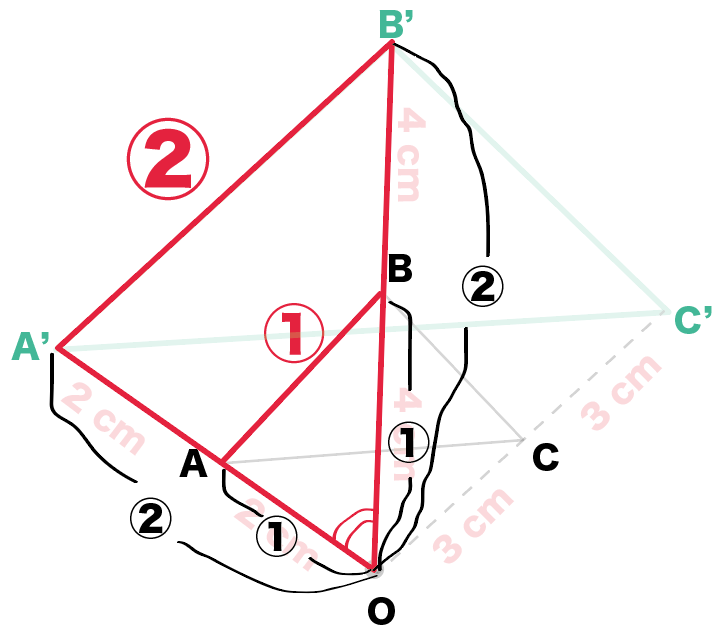



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




全ての放物線が相似であることの証明 高校数学の美しい物語



中3です 円の相似について質問です 全ての円は相似である というように Yahoo 知恵袋
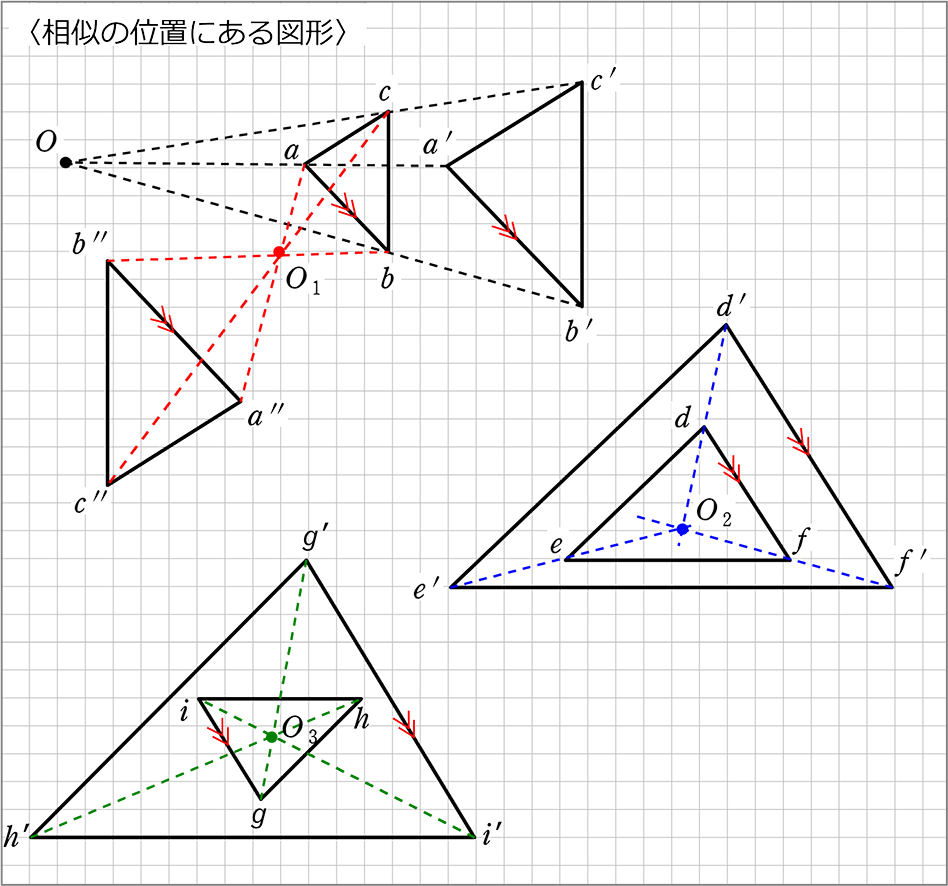



中学数学 図形の相似




中学数学 図形の相似
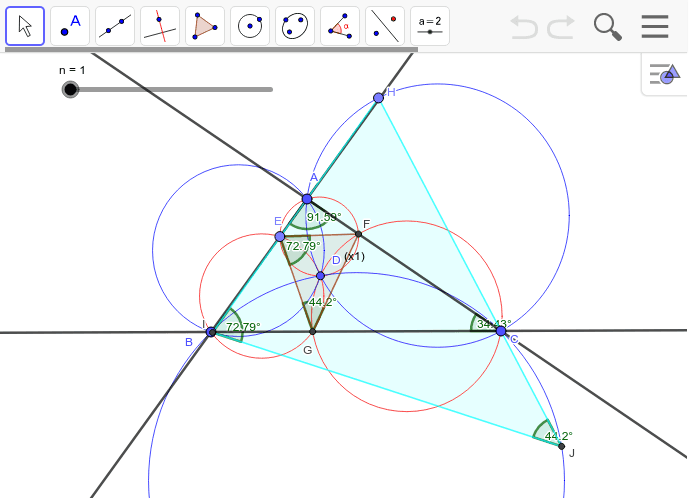



心を中心とする三円 Geogebra




中3 相似の位置と相似の中心 Youtube



平面の変換
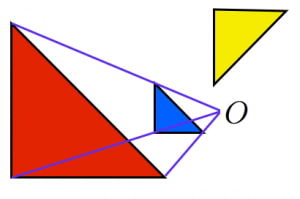



全ての放物線が相似であることの証明 高校数学の美しい物語



平面の変換




B Bar8cm C E Bar10cm G Lihat Cara Penyelesaian Di Qanda
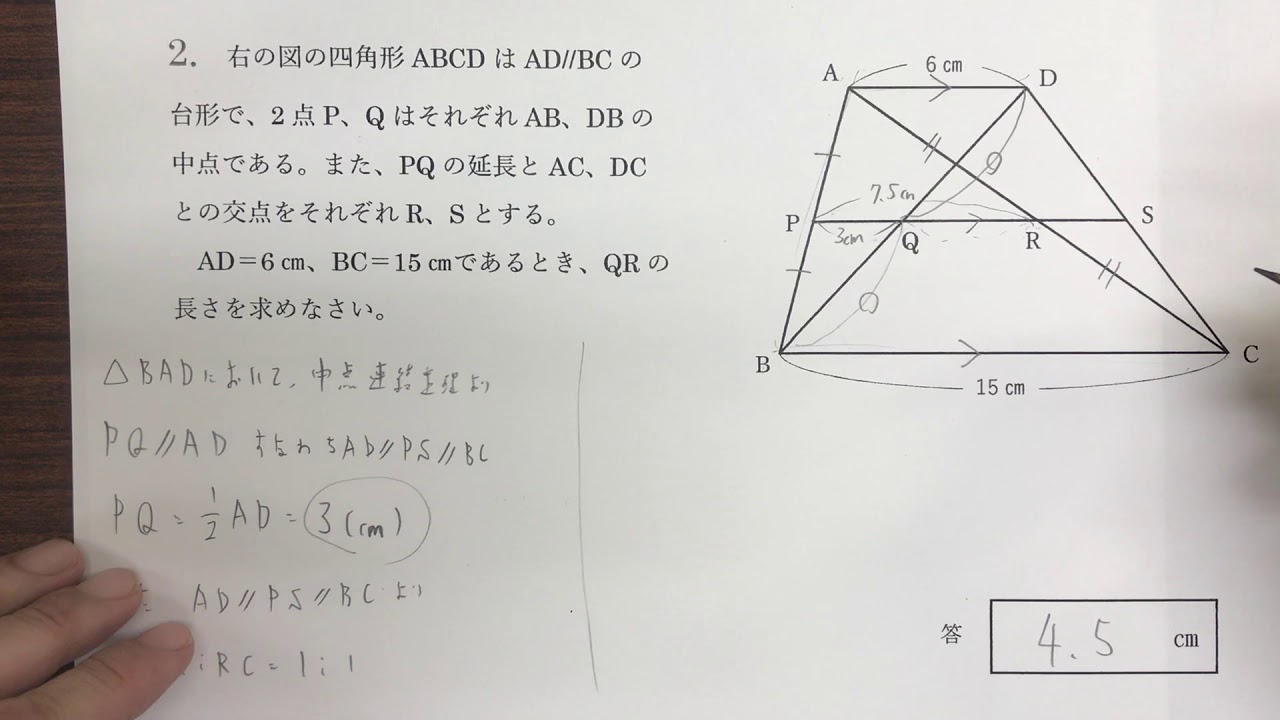



図形 証明 応用問題 相似中心 大問2 中学数学単元別強化教材 これから 図形 紹介動画 3年生2学期レベル Youtube



0 件のコメント:
コメントを投稿